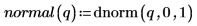Пример. Z-показатель вектора данных

Функции > Статистика > Распределения вероятностей > Пример. Z-показатель вектора данных

Вычислите Z-показатель для вектора данных с нормальным распределением с известным среднеквадратическим отклонением для совокупности.

1. Определите набор данных для анализа.

Щелкните для копирования этого выражения

2. Рассчитайте среднее значение выборки m_s.

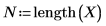
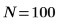
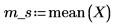
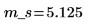
3. Определите уровень значимости, среднеквадратическое отклонение для совокупности и предлагаемое среднее для совокупности.

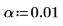
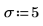
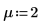
4. Рассчитайте z-значение.

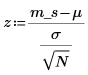
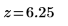
5. Определите нулевую и альтернативную гипотезы для двустороннего критерия.

H0: m = μ

H1: m ≠ μ

6. Используйте функцию pnorm, чтобы вычислить p-значение и проверить гипотезу. В этом примере все логические выражения дают 1, если истинной оказывается нулевая гипотеза (H0 не отклоняется).

<region id="ID0EPDZBB" top="883.20000000000016" left="38.400000000000006" height="25.6" width="185.36333333333334" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="84">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">P</id>
      <apply>
        <mult />
        <real>2</real>
        <parens>
          <apply>
            <minus />
            <real>1</real>
            <apply>
              <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">pnorm</id>
              <sequence>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">z</id>
                <real>0</real>
                <real>1</real>
              </sequence>
            </apply>
          </apply>
        </parens>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

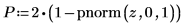
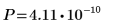
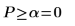
Существует вероятность 4.11*10-10, что критерий значимости больше, чем наблюдаемый критерий, при условии что нулевая гипотеза истинна. Сравнение p-значения и уровня значимости свидетельствует, что альтернативная гипотеза является истинной.

7. Используйте функцию qnorm, чтобы вычислить пределы критической области и проверить гипотезу.

<region id="ID0E4GZBB" top="1171.2000000000003" left="38.400000000000006" height="47.2" width="163.91666666666669" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="90">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">crit</id>
      <apply>
        <absval />
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">qnorm</id>
          <sequence>
            <apply>
              <div />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">α</id>
              <real>2</real>
            </apply>
            <real>0</real>
            <real>1</real>
          </sequence>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

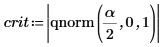
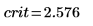
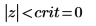
Отклоните нулевую гипотезу. Очевидно, что среднее значение не равно μ.

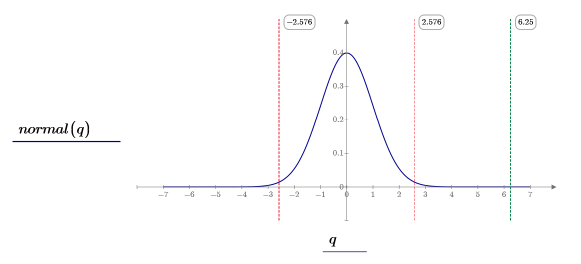
8. Используйте функцию dnorm, чтобы вычислить и построить график стандартного нормального распределения (синий), границ критической области (красный) и z-оценку (зеленый).

<region id="ID0EHKZBB" top="1382.4" left="38.400000000000006" height="25.6" width="196.62333333333334" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="96">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="VARIABLE" xml:space="preserve">normal</id>
        <boundVars>
          <id labels="VARIABLE" xml:space="preserve">q</id>
        </boundVars>
      </function>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">dnorm</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">q</id>
          <real>0</real>
          <real>1</real>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Похожие темы

Нормальное распределение

Было ли это полезно?