Пример. Использование единиц измерения с функциями полиномиальной интерполяции
1. Определите два входных вектора и независимую переменную.
 |
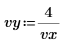 |
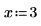 |
2. Определите единицы измерения.
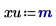
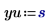
3. Вычислите входные векторы и входную переменную.
 |  | 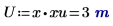 |
Единица измерения независимой переменной U должна соответствовать единице измерения вектора первого аргумента. |
Полиномиальная интерполяция
1. Используйте функцию polyint, чтобы вычислить интерполяционную функцию при указанных значениях независимой переменной.
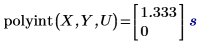
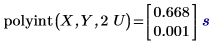
Поиск U во входном векторе X приводит к сопоставлению, и соответствующее точное значение в векторе Y равняется 1.333 с нулевой ошибкой. Однако 2U не имеет точного совпадения в X, и это приводит к интерполированному значению с ненулевой ошибкой.
2. Используйте функцию length, чтобы определить длину входных векторов, а затем создайте короткую программу, чтобы вычислить функции интерполяции в разных точках. Отобразите точки интерполяции в первом столбце и значения ошибок во втором столбце.
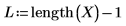

Переменная u должна быть скаляром, а единица измерения m добавляется как часть аргумента функции.
3. Сохраните точки интерполяции и значения ошибок в двух отдельных векторах.
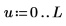
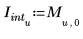
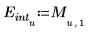
4. Постройте график точек интерполяции вместе с огибающей ошибок.
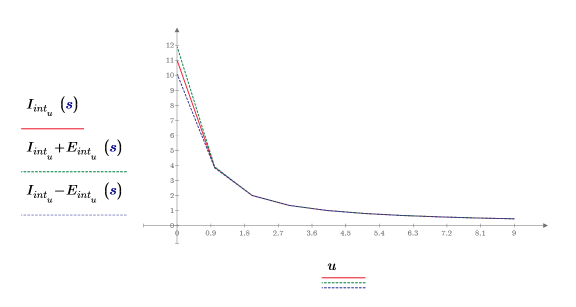
Ошибки начинаются с относительно большой, но затем становится пренебрежимо малыми после второй точки интерполяции.
Итерация полиномами
1. Используйте функцию polyiter, чтобы вычислить функцию итерации при указанном значении независимой переменной, максимальном числе итераций и допуске.
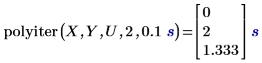
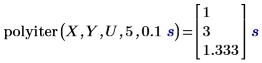
• Выполнение алгоритма останавливается, когда рассчитанные точки данных после двух последних итераций удовлетворяют допуску или когда достигается максимальное разрешенное число итераций. • Первый результат показывает, что функция итерации не сходится после максимального разрешенного числа итераций, поэтому возвращается соответствующий элемент в вектореY. • Второй результат показывает, что функция итерации сходится после третьей итерации без достижения максимального разрешенного числа пяти итераций. |
2. Используйте короткую программу, чтобы вычислить функцию итерации в десяти разных точках. Используйте функцию augment, чтобы добавить значение ошибки в четвертый столбец возвращаемой матрицы, которая показывает статус схождения в первом столбце, число использованных итераций во втором столбце и итерируемые значения в третьем столбце.

3. Сохраните точки интерполяции и значения ошибок в отдельных векторах.
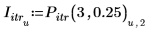
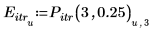
4. Постройте график точек итерации для 3 итераций и ошибки 0.25.
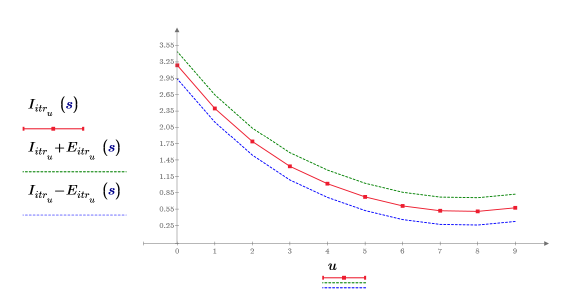
Значение ошибки является постоянным в каждой точке интерполяции.
5. Сравните возвращенные результаты интерполяции и итерации, когда заданы максимальное число итераций 3 и ошибка 0.25.
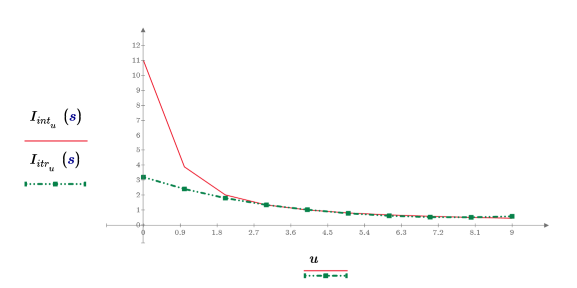
6. Покажите, что результаты интерполяции идентичны результатам итерации, когда заданы большое количество итераций и нулевая ошибка.
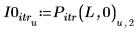
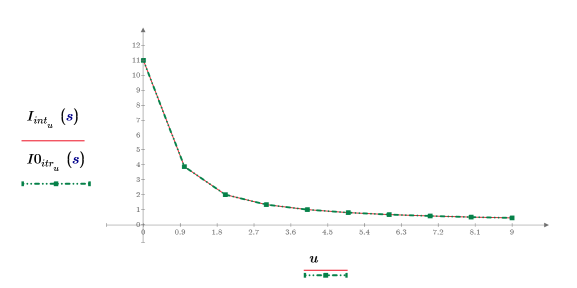
Максимальное число итераций должно быть меньше, чем длина входных векторов.