Пример. Критерий Стьюдента для средних значений нормально распределенной совокупности

Функции > Статистика > Распределения вероятностей > Пример. Критерий Стьюдента для средних значений нормально распределенной совокупности

Проверить гипотезу: две нормально распределенные совокупности имеют равные средние значения.

1. Задайте наборы данных для сравнения

Щелкните для копирования этого выражения

2. Соберите статистику выборки.

Число элементов в выборке для каждого набора данных.	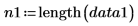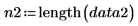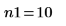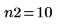<region id="ID0EPK1BB" top="403.20000000000005" left="38.400000000000006" width="137.98000000000002" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="91"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="">n1</id> <apply> <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">length</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">data1</id> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region> <region id="ID0EYK1BB" top="441.60000000000008" left="38.400000000000006" width="137.98000000000002" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="95"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="">n2</id> <apply> <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">length</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">data2</id> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0ENL1BB" top="403.20000000000005" left="384.00000000000006" width="65.516666666666666" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="93"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region> <region id="ID0E2L1BB" top="441.60000000000008" left="384.00000000000006" width="65.516666666666666" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="97"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
Выборочные средние значения.	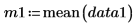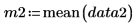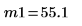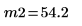<region id="ID0EAN1BB" top="480.00000000000006" left="38.400000000000006" width="136.66000000000003" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="99"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="">m1</id> <apply> <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">mean</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">data1</id> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region> <region id="ID0EON1BB" top="518.40000000000009" left="38.400000000000006" width="136.66000000000003" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="103"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="">m2</id> <apply> <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">mean</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">data2</id> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EDO1BB" top="480.00000000000006" left="384.00000000000006" width="82.250000000000014" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="101"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m1</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region> <region id="ID0ERO1BB" top="518.40000000000009" left="384.00000000000006" width="82.250000000000014" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="105"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m2</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
Выборочные среднеквадратические значения.	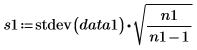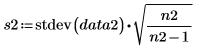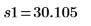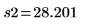<region id="ID0EWP1BB" top="614.40000000000009" left="38.400000000000006" width="197.0459999702374" height="50.065333527326587" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="111"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="">s1</id> <apply> <mult /> <apply> <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">stdev</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">data1</id> </apply> <apply> <nthRoot /> <placeholder /> <apply> <div /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id> <apply> <minus /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id> <real>1</real> </apply> </apply> </apply> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region> <region id="ID0EEQ1BB" top="672.00000000000011" left="38.400000000000006" width="197.0459999702374" height="50.065333527326587" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="115"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="">s2</id> <apply> <mult /> <apply> <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">stdev</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">data2</id> </apply> <apply> <nthRoot /> <placeholder /> <apply> <div /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id> <apply> <minus /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id> <real>1</real> </apply> </apply> </apply> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EZQ1BB" top="614.40000000000009" left="384.00000000000006" width="90.876666666666679" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="113"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">s1</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region> <region id="ID0EHR1BB" top="672.00000000000011" left="384.00000000000006" width="90.876666666666679" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="117"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">s2</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
Степени свободы при комбинировании двух средних.	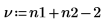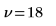<region id="ID0EMS1BB" top="556.80000000000007" left="38.400000000000006" width="105.12666666666667" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="107"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="*">ν</id> <apply> <minus /> <apply> <plus /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id> </apply> <real>2</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EBT1BB" top="556.80000000000007" left="384.00000000000006" width="56.493333333333339" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="109"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">ν</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
Среднеквадратическая ошибка расхождения в наборах данных.	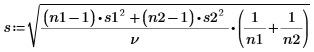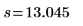<region id="ID0EEU1BB" top="729.60000000000014" left="38.400000000000006" width="313.71933330357075" height="52.217333527326588" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="119"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="*">s</id> <apply> <nthRoot /> <placeholder /> <apply> <mult /> <apply> <div /> <apply> <plus /> <apply> <mult /> <parens> <apply> <minus /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id> <real>1</real> </apply> </parens> <apply> <pow /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">s1</id> <real>2</real> </apply> </apply> <apply> <mult /> <parens> <apply> <minus /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id> <real>1</real> </apply> </parens> <apply> <pow /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">s2</id> <real>2</real> </apply> </apply> </apply> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">ν</id> </apply> <parens> <apply> <plus /> <apply> <div /> <real>1</real> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id> </apply> <apply> <div /> <real>1</real> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id> </apply> </apply> </parens> </apply> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EYU1BB" top="729.60000000000014" left="384.00000000000006" width="82.896666666666675" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="121"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">s</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

3. Определите уровень значимости.

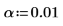
4. Вычислите критерий значимости.

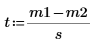
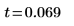
5. Задайте нулевую и альтернативную гипотезы.

H0: m1 ≤ m2

H1: m1 > m2

6. Рассчитайте p-значение и проверьте гипотезу. В этом примере все логические выражения дают 1, если истинной оказывается нулевая гипотеза (H0 не отклоняется).

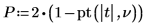
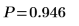
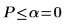
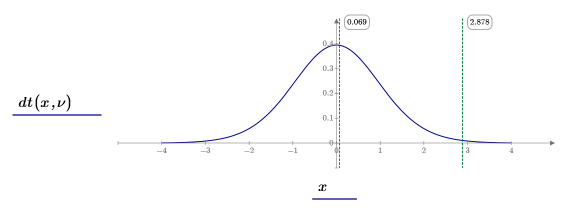
Существует вероятность 0.946, что критерий значимости больше, чем наблюдаемый критерий, при условии, что нулевая гипотеза истинна. Сравнение p-значения с уровнем значимости показывает, что альтернативная гипотеза не может быть истинной.

7. Рассчитайте предел критической области и проверьте гипотезу.

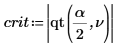
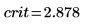
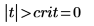
Примите нулевую гипотезу. Нет данных, подтверждающих, что m1 больше m2.

8. Нанесите на график распределение Стьюдента (синий), границу критической области (зеленый) и статистику критерия (красный).

<region id="ID0EEB2BB" top="1804.8000000000002" left="38.400000000000006" width="580" height="211.19999999999996" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true" background-type="white">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace num-of-points="500" resultRef="141">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-4" end="4">
          <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">crit</id>
            <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">t</id>
          </markers>
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="152">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math resultRef="153">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="147">
              <real xmlns="http://schemas.mathsoft.com/math50">-4</real>
            </startValue>
            <real xmlns="http://schemas.mathsoft.com/math50">-3</real>
            <endValue resultRef="151">
              <real xmlns="http://schemas.mathsoft.com/math50">4</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.4">
          <axisLine position="origin" positionticmark="4" legendWidth="106.173333333333" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="160">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">dt</id>
                  <sequence>
                    <id xml:space="preserve">x</id>
                    <id xml:space="preserve">ν</id>
                  </sequence>
                </apply>
              </math>
              <math resultRef="161">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="155">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <real xmlns="http://schemas.mathsoft.com/math50">0.1</real>
            <endValue resultRef="159">
              <real xmlns="http://schemas.mathsoft.com/math50">0.4</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Похожие темы

Распределение Стьюдента

Было ли это полезно?