Пример. Символьные решения уравнений
Символьные решения уравнений с одной или несколькими неизвестными.
Решение одного уравнения
1. Введите следующее уравнение:
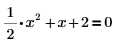
2. Вставьте оператор аналитического преобразования, введите ключевое слово solve в местозаполнитель и нажмите клавишу ВВОД.
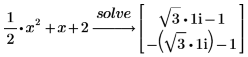
Поскольку правая часть уравнения равняется 0, нет необходимости вводить часть =0 выражения. |
3. Введите константу 2 в десятичный формат в виде 2.0, чтобы возвращать ответ в формате с плавающей точкой.
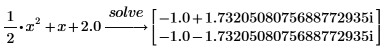
4. Решите уравнение с одной переменной:
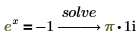
5. Решите уравнение с несколькими переменными:
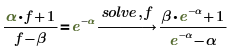
Когда уравнение содержит несколько переменных, необходимо указать, относительно какой переменной его следует решать. |
6. Найдите решение для полинома четвертого порядка:

Приведенный выше результат показывает, что аналитическое решение полинома четвертого порядка дает четыре численных решения. |
7. Найдите корни полинома с параметрическими коэффициентами:
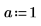
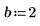
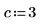
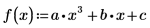
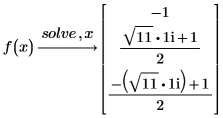
Решение систем уравнений и равенств
Можно совместно решить несколько уравнений и равенств как систему уравнений, сгруппировав их в виде вектора.
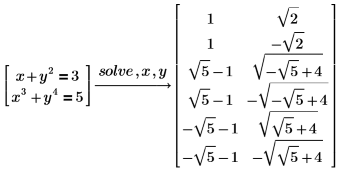
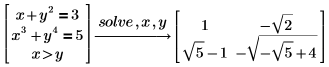
Решение полиномов в радикалах
По умолчанию PTC Mathcad решает полиномиальные уравнения до 4-й степени через радикалы. Решения выражаются через радикалы с использованием обычных арифметических операторов.
1. Найдите решение для следующего полинома:
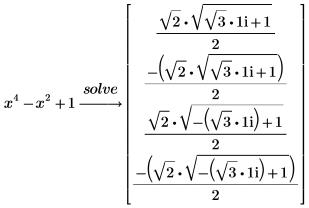
Математик Галуа в девятнадцатом веке доказал, что имеются полиномы степени 5 и выше, которые невозможно решить через радикалы. Для таких полиномов PTC Mathcad возвращает численную аппроксимацию корней. |
2. Найдите решение для полинома степени 5:

Приведенный выше результат показывает, что аналитическое решение полинома четвертого порядка дает четыре численных решения. |
Предположения об области существования переменной
Используйте ключевое слово assume, чтобы делать предположения об области существования переменной в задаче (например, что переменная является вещественным числом).
1. Решите уравнение с допущением, что переменная является вещественным числом:
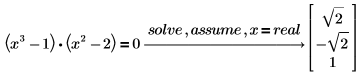
PTC Mathcad возвращает только действительные решения уравнения. |
2. Используйте RealRange, чтобы найти действительные решения в диапазоне (0, 2).
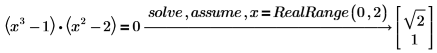
3. Введите x=integer, чтобы найти только целочисленные решения.
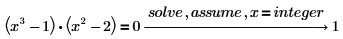
4. Введите assume, чтобы ограничить область существования переменной в аналитическом преобразовании.
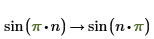
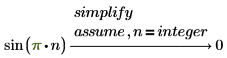
Возвращение подробных решений уравнений
Добавьте модификатор fully после solve, чтобы получить подробные решения уравнений.
1. Используйте функцию clear.sym, чтобы очистить предыдущее символьное значение a:
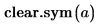
2. Используйте fully, чтобы получать значения a, для которых решение является допустимым.
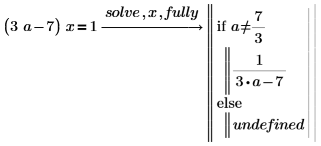
3. Используйте подробный результат, чтобы определить функцию.
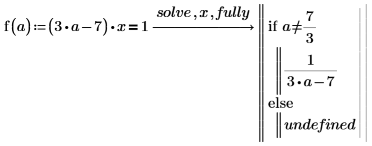
4. Вычислите функцию при a=3 и a=7/3:
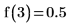
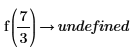
Уравнения с периодическими решениями
Для уравнений с периодическим решением PTC Mathcad возвращает единственное решение с последующим выражением для добавления целочисленного периода к первому решению.
1. Используйте fully, чтобы вычислить sin(x).
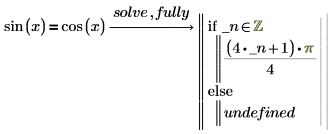
Выражение, следующее за оператором if, означает pi/4 плюс все кратные целые числа pi. PTC Mathcad вставляет новую сгенерированную переменную _n, представляющую произвольное целое число. Символ подчеркивания вставляется перед сгенерированной переменной во избежание конфликта имен с другими переменными, которые могли быть определены в других местах в документе. |
2. Добавьте модификатор using, за которым следует уравнение, записанное с логическим оператором равенства, чтобы приравнять созданную переменную к новой переменной.
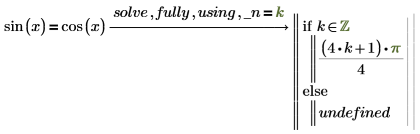
Если переменная, указанная после ключевого слова using, не является сгенерированной переменной, которую возвращает solve, PTC Mathcad возвращает ошибку.