Пример. Спектральный анализ
Используйте функции coherence, cspectrum, pspectrum и snr для расчета когерентности, взаимного спектра, спектра мощности и отношения сигнал-шум для сигнала или пар сигналов.
Описание этой процедуры усреднения взято из книги Samuel Stearns and Ruth David, Signal Processing Algorithms (Алгоритмы обработки сигналов), Prentice-Hall, Inc..
Спектр мощности - использование ДПФ
Для длинных временных рядов, в которых значения всего нескольких точек данных соответствуют сигналу, желательно получить спектр мощности, показывающий частоты значений сигнала, а не шума или нулевых значений.
1. Определите ширину окна.
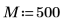
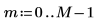
2. Определите два возможных окна, w1 и w2, в которых сигнал не является нулевым.
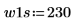 | 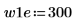 | 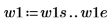 |
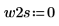 | 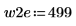 | 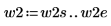 |
3. Задайте для ширины окна одно из двух возможных значений.
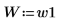
4. Определите частоты сигнала и выборки.
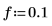
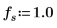
5. Используйте функцию sin, чтобы определить сигнал внутри и снаружи выбранного окна.
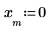
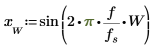
6. Постройте график сигнала.
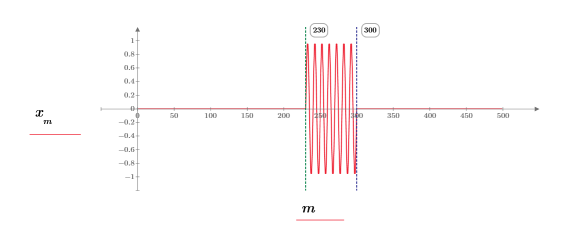
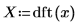
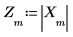
8. Постройте график результирующей функции в частотной области.
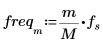
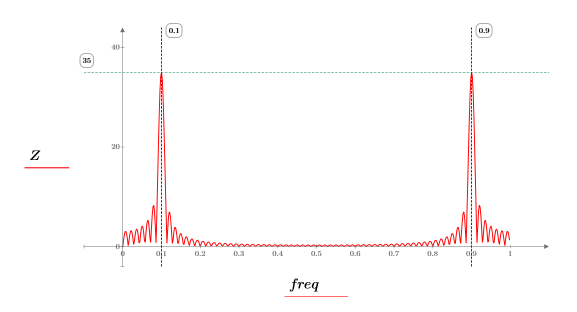
◦ Для чистого синусоидального сигнала величина коэффициентов ДПФ дает хорошую оценку спектра мощности. Но в этом случае ДПФ сигнала является частотным содержимым структурированного сигнала, свернутого с преобразованием прямоугольного окна (функция sinc).
◦ Если задать W= w2 (шаг 3), ширина окна, в котором существует синусоидальный сигнал, увеличивается с 230-300 до 0-499 (коэффициент 7.143x), в результате чего величина двух пиков возрастает с 35 до 250 (также с коэффициентом 7.143x).
◦ Частоты, при которых возникают пики, не изменяются.
Спектр мощности - использование pspectrum
Функция pspectrum разбивает исходный временной ряд на перекрывающиеся сегменты. Каждый из этих сегментов преобразуется ДПФ, а коэффициенты преобразованных величин усредняются. Если длина сегментов по масштабу совпадает с явлением, анализируемым в сигнале, функция pspectrum возвращает хорошую аппроксимацию величины компонентов значимых частей исходного временного ряда.
Как правило, длина сигнала должна составлять по меньшей мере n + 1.
1. Определите длину сигнала, коэффициент перекрытия и тип окна (трапециевидное).
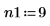 | 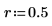 | 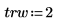 |
2. Используйте функцию pspectrum, чтобы вычислить спектр мощности x. Для этого x делится на n1 перекрывающихся сегментов с коэффициентом перекрытия r и кадрированием каждого сегмента с помощью трапециевидного окна.
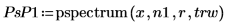
3. Используйте функции floor и length, чтобы показать, что длина интервала является наибольшим числом L, для которого:
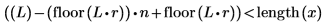
4. Постройте график спектра с нормализованной частотной осью (1 представляет частоту выборки).
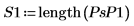
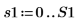
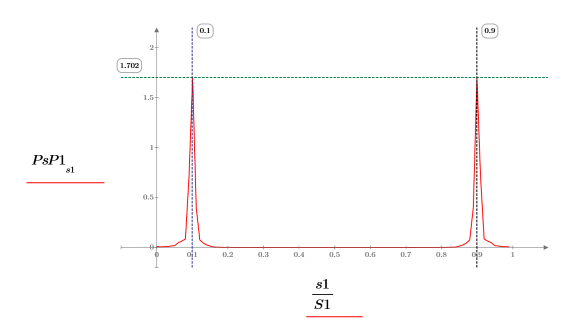
5. Рассчитайте среднюю мощность в спектре.
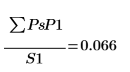
Она приблизительно равна среднеквадратичному значению сигнала x.
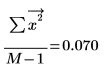
pspectrum с белым шумом
Рассчитайте спектр мощности сигнала, содержащего белый шум. Создайте два таких сигнала, поскольку второй сигнал нужен для расчета взаимного спектра. Для сужения блока данных используйте окно Хэмминга.
1. Задайте ширину сигнала.
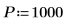
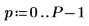
2. Используйте функции sin и rnd, чтобы определить два сигнала с общей частотой fc. Функция rnd возвращает вектор однородно распределенных случайных чисел между 0 и указанным числом, благодаря чему сохраняется различие между сигналами.
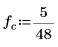
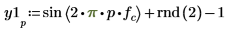
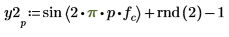
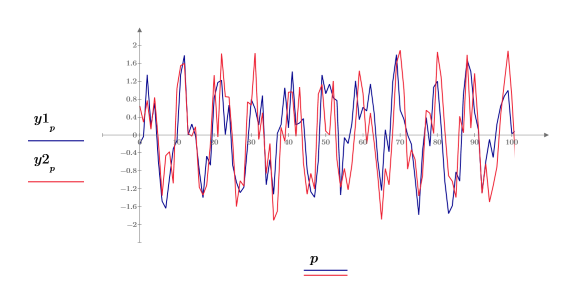
3. Постройте график первых 100 выборок двух сигналов.
4. Используйте функцию pspectrum, чтобы получить спектр мощности y1. Для этого разделите его на 40 перекрывающихся сегментов с коэффициентом перекрытия 0.5 и кадрированием каждого сегмента с помощью окна Хэмминга.
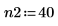 | 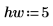 |
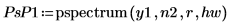 | |
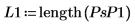 | 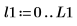 |
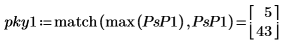
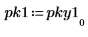
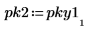
6. Постройте график спектра в децибелах. С помощью маркеров отметьте общую частоту и максимальное значение в децибелах.
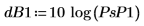
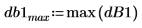
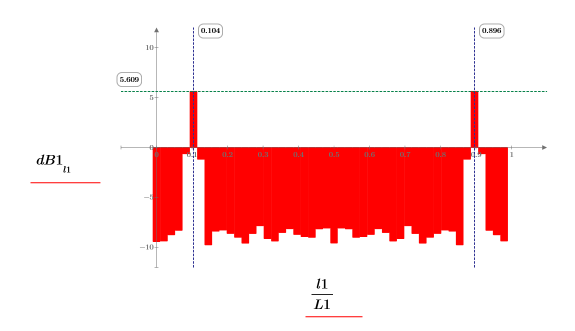
График показывает, что вся мощность сигнала относится к общим частотам fc и 1-fc.
7. Рассчитайте мощность шума.
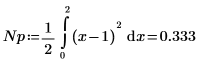
8. Рассчитайте коэффициент передачи мощности шума в дБ.
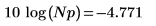
9. Рассчитайте высоту, исходя из того факта, что вышеприведенные две частотные выборки, поделенные на длину спектра, должны в результате давать среднюю мощность компонента синусоиды, которая равна 0.5.
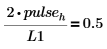 | Или: | 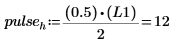 |
10. Сравните теоретические и фактические высоты в децибелах.
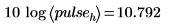
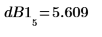
Функция cspectrum
Обычно взаимный спектр используется для обнаружения сходства в двух сигналах, например для сравнения известного речевого сигнала (скажем, гласной "я") с неизвестным речевым сигналом (скажем, словом "яблоко"), чтобы увидеть, присутствует ли известный речевой сигнал в неизвестном. Так же, как спектр мощности временного ряда подобен своей автокорреляции, взаимный спектр двух временных рядов подобен их взаимной корреляции. Для стационарных случайных последовательностей функции спектра возвращают те же значения, что и функции корреляции.
1. Примените функцию cspectrum к сигналам y1 и y2, используя 40 перекрывающихся сегментов с коэффициентом перекрытия 0.5 и кадрируя каждый сегмент с помощью трапециевидного окна.
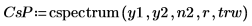
2. Постройте график спектра в децибелах.
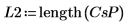 | 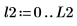 |
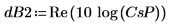 | |
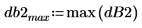 |
3. Постройте график взаимного спектра, учитывая, что он является комплексным, и поэтому протокол должен применяться к величине.
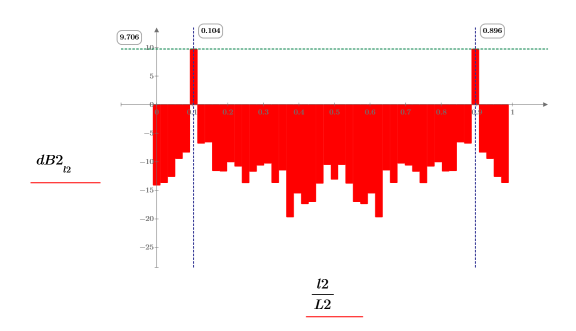
Взаимный спектр y1 и y2 демонстрирует пик на общих частотах fc и 1- fc.
Функции coherence и snr
Функция coherence измеряет линейную зависимость одного сигнала от другого и равна квадрату величины взаимного спектра двух сигналов, деленному на оба спектра мощности. Значение находится в диапазоне от 0 до 1. Значение 1 функции когерентности указывает, что оба сигнала имеют в этом диапазоне частот выраженные компоненты, свободные от шума. Значение 0 указывает, что в этом диапазоне частот в основном наблюдается шум.
Функция отношения сигнал-шум snr равна функции coherence, деленной на единицу минус функция coherence, и максимизируется там, где два сигнала обладают сильными компонентами в любой составляющей полосе, пропорциональными отношению мощностей сигналов и мощности шума датчика или фонового шума.
1. Примените функцию coherence к сигналам y1 и y2, используя 40 перекрывающихся сегментов с коэффициентом перекрытия 0.5 и кадрируя каждый сегмент с помощью окна Хэмминга.
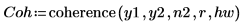 | |
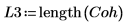 | 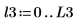 |
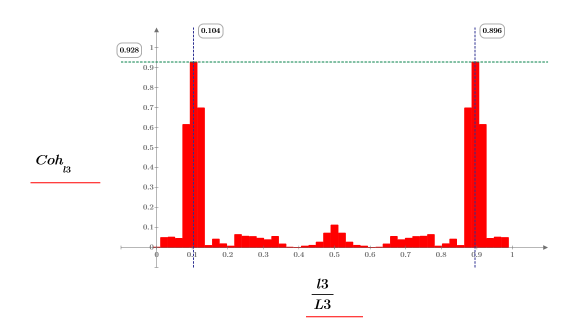
2. Постройте график функции coherence. С помощью маркеров отметьте общую частоту и максимальное значение.
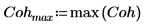
3. Примените функцию snr к сигналам y1 и y2, используя 40 перекрывающихся сегментов с коэффициентом перекрытия 0.5 и кадрируя каждый сегмент с помощью окна Хэмминга.
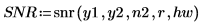 | |
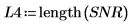 | 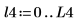 |
4. Постройте график функции отношения сигнал-шум. С помощью маркеров отметьте общую частоту и максимальное значение.
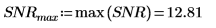
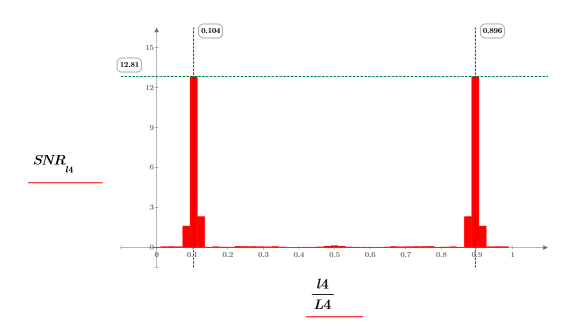
Обе функции coherence и snr показывают максимальное значение на одиночных частотных составляющих двух сигналов с добавленным шумом, представленным двумя столбиками меньшего размера с каждой стороны.