Пример. Анализ остатка
Рассчитайте остатки набора данных, чтобы проверить, является ли набор линейно распределенным. Перед использованием регрессионной модели в целях прогнозирования нужно проверить, удовлетворяются ли допущения линейной модели.
• Ошибки не должны быть коррелированы.
• Для любого заданного значения X ошибки должны быть нормально распределены со средним, равным нулю, и постоянной дисперсией.
Стандартизированные остатки
Чтобы интерпретировать относительную величину остатков, их можно стандартизировать. Остатки нужно разделить на оценочное среднеквадратическое отклонение ошибок.
1. Определите следующий набор данных:
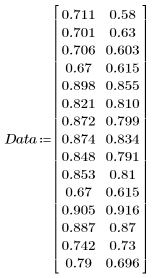
2. Постройте график набора данных.
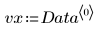
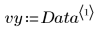
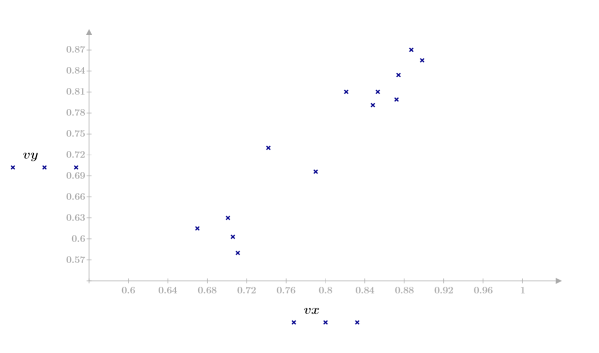
Данные выглядят линейными. Это подтверждается коэффициентом корреляции, близким к 1:
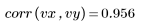
3. Определите линию наилучшего приближения:
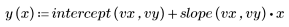
4. Выделите значения приближения из измеренных значений.
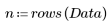
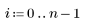
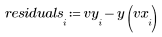
5. Разделите остатки на среднеквадратическую ошибку оценки.
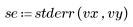
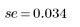
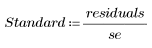
Стьюдентизированные остатки
Стьюдентизированные остатки, или скорректированные стьюдентизированные остатки, — это другая часто используемая оценка среднеквадратической ошибки. Эта оценка корректирует расстояние между каждым значением x и средним x.
1. Рассчитайте расстояние между значениями и средним.
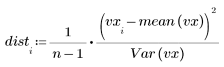
2. Определите среднеквадратическое отклонение, усиленное для каждого остатка.

3. Определите стьюдентизированные остатки:
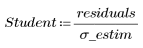
Стьюдентизированные остатки точнее стандартизированных остатков, потому что они учитывают любые различия между точками в дисперсии ошибки. Тем не менее, значения остатков обычно близки:
 |  |
4. Вызовите функцию polyfitstat. Выведите изображение подматрицы диагностики наблюдения, содержащей стьюдентизированные остатки.
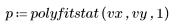
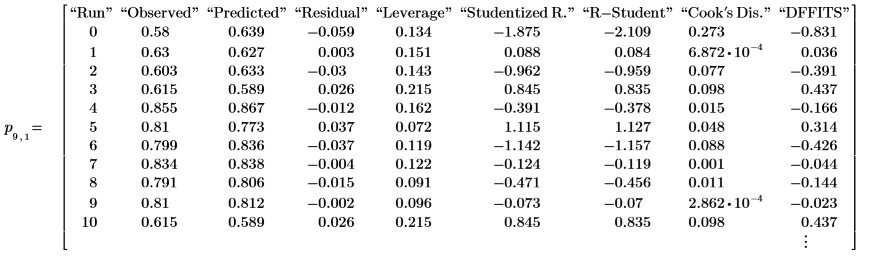
Проверка на линейность
Проверьте, что набор Data является линейно связанным. Создайте противоположный пример, используя случайную выборку с криволинейной связью. Если данные линейно связаны, а ошибки нормально распределены, в графиках разброса не прослеживаются заметные модели. Точки случайным образом разбросаны вокруг гипотетического нулевого среднего значения ошибки.
1. Постройте график остатков относительно значений x и относительно прогнозированных значений y.
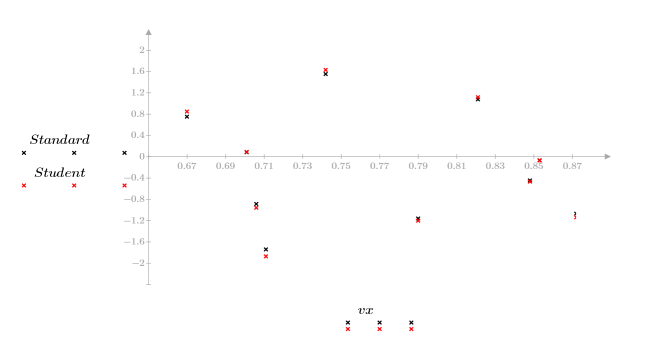
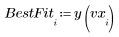
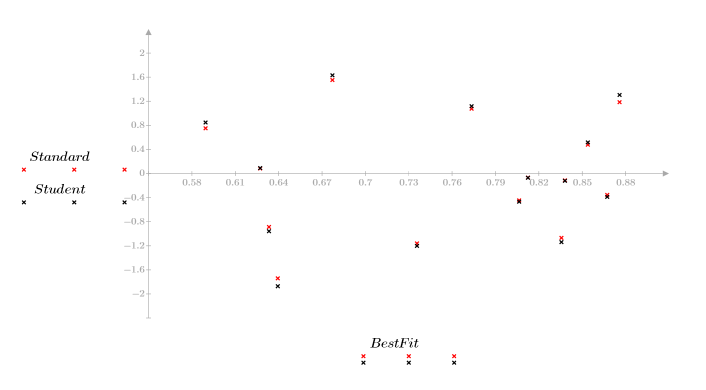
Отсутствие модели распределения остатков указывает на то, что данные линейно связаны.
2. Создайте случайную выборку точек с квадратичной связью.
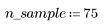
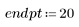
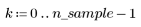
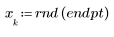
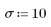
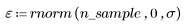
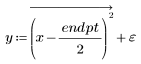
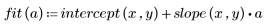
3. Постройте график относительной величины остатков.
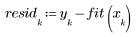
Квадратичная модель распределения данных отражается в графике разброса остатков. Эти данные не являются линейно связанными.
Проверка дисперсий постоянной ошибки
В наборе Data обнаружено отсутствие модели в дисперсиях ошибки. Создайте противоположный пример, в котором данные выглядят линейными, но дисперсии ошибки не распределены нормально, а график разброса остатков показывает увеличение или уменьшение расхождения слева направо.
1. Создайте случайную выборку точек, разброс которых возрастает слева направо.
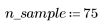
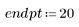
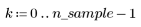
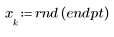
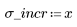
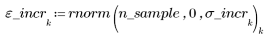
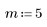
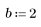
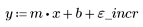
2. Рассчитайте линию наилучшего приближения. Постройте график случайного набора данных и функции аппроксимации.
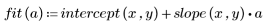
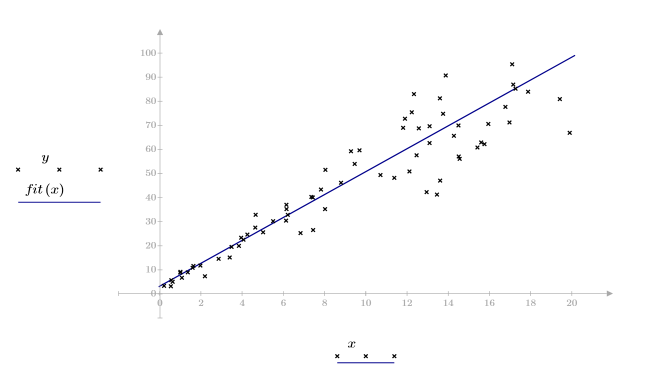
Коэффициент корреляции, близкий к 1, указывает на то, что данные линейно связаны:
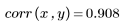
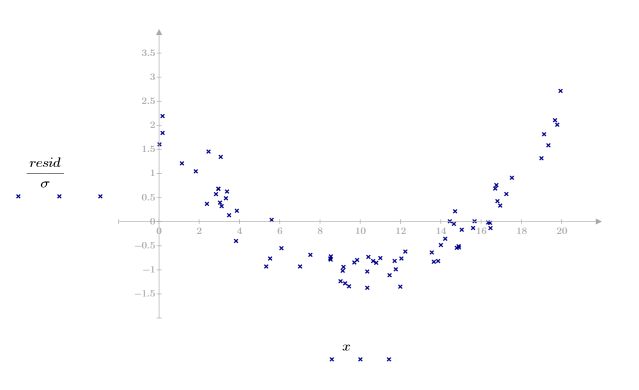
3. Постройте график относительной величины остатков.
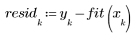
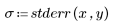
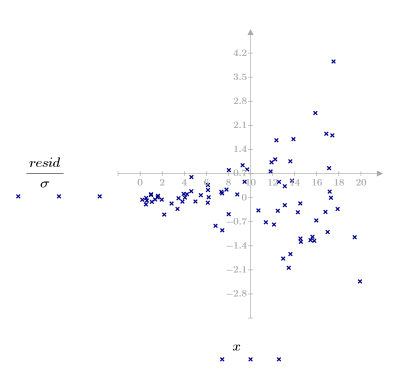
График разброса остатков не выглядит случайно распределенным. Разброс точек в графике остатков растет слева направо.
Проверка корреляции ошибок
Проверку корреляции смежных элементов ошибок в модели линейной регрессии можно провести с помощью статистики Дурбина-Уотсона.
Рассчитайте статистику Дурбина-Уотсона для набора Data:
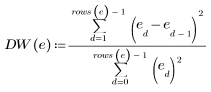
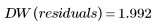
Значения статистики Дурбина-Уотсона лежат в диапазоне от 0 до 4. Если смежные элементы не скоррелированы, то значение Дурбина-Уотсона приближено к 2. Значения Дурбина-Уотсона, меньшие 2, указывают на положительную корреляцию смежных элементов, а значения, которые больше 2, указывают на отрицательную корреляцию.
Статистика Дурбина-Уотсона используется при расчете B-сплайнов методом наименьших квадратов. К сожалению, статистика Дурбина-Уотсона не позволяет обнаружить корреляции более высокого порядка (несмежных элементов). Корреляция этих типов редко встречается без корреляции между смежными ошибками.
Статистика Дурбина-Уотсона является одной из статистик, возвращаемых функцией polyfitstat:
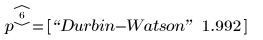
Проверка на нормальность
Проверьте, является ли набор Data нормально распределенным, создав график нормального распределения стандартизированных остатков.
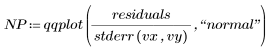
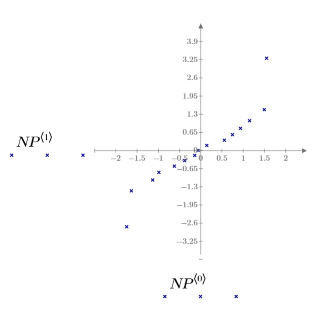
График нормального распределения имеет сходство с прямой линией. Поэтому ошибки приблизительно нормально распределены. Поскольку графики нормального распределения могут быть чувствительны к другим нарушениям допущений, таким как неравенство дисперсий ошибки, проверку на нормальность лучше всего проводить в последнюю очередь.