Пример. Плотность вероятности и кумулятивное распределение вероятностей
1. Задайте среднее значение и среднеквадратическое отклонение для нормального распределения.
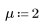
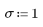
2. Постройте график плотности вероятности (синяя кривая) и кумулятивное распределение вероятностей (красная и черная кривые) для нормальных распределений.
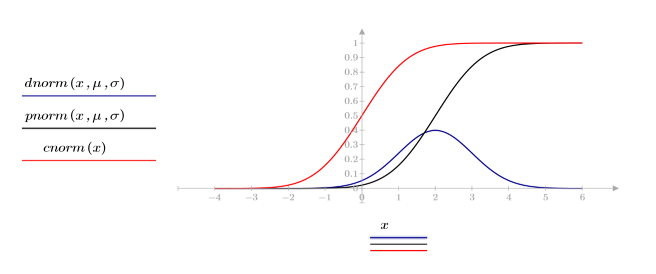
Функция dnorm рассчитывает плотность вероятности x для нормального распределения со средним значением μ и среднеквадратическим отклонением σ. Функция pnorm рассчитывает кумулятивное распределение вероятностей для нормального распределения. Функция cnorm — это кумулятивное распределение вероятностей для нормального распределения, где μ = 0 и σ = 1.
3. Используйте функцию qnorm для расчета значения x, при котором площадь под кривой от ∞ до x равна половине площади под всей кривой.
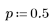
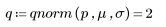
В этом случае значение x равно среднему значению, что подтверждается следующей формулой:
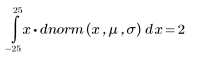
Плотность вероятности для значения q легко найти с помощью функции pnorm, которая является обратной для функции qnorm:
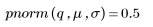
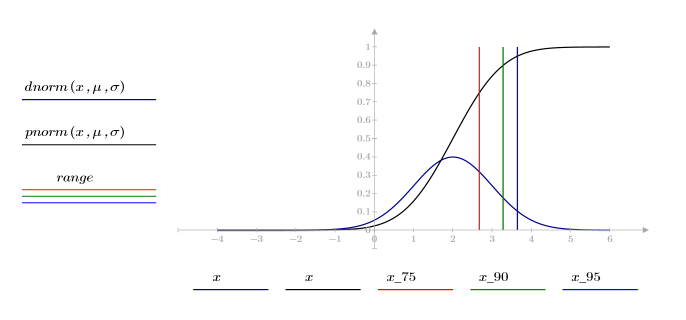
4. Используйте функцию qnorm для поиска 75-го, 90-го и 95-го процентилей нормального распределения.
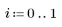
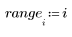
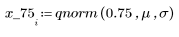
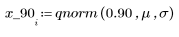
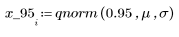
5. Постройте график распределения вероятностей (синяя кривая) и кумулятивного распределения вероятностей (черная кривая) для нормального распределения с добавлением процентилей, вычисленных выше (75 % — красная, 90 % — зеленая, 95 % — синяя).