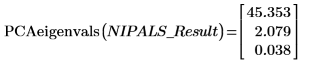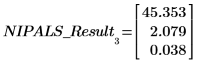Пример. Анализ главных компонентов 1
Используйте функции Nipals, loadings, scores, PCAeigenvals и PCAvariance для выполнения анализа главных компонентов (PCA).
Функция Nipals
1. Задайте набор данных, в котором каждый столбец соответствует одной переменой.


2. Постройте график набора данных.
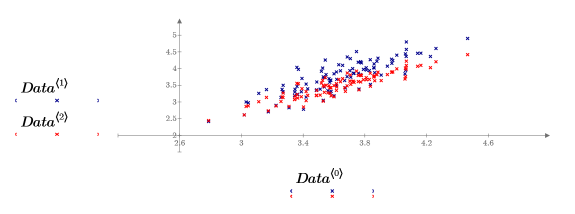
На этом графике плоскости x-y и x-z накладываются одна на другую, чтобы выявить закономерности в данных. В сущности данные представляют собой эллиптическое облако точек, которые находятся практически в одной плоскости. Три переменные линейно связаны между собой, а отклонение от плоскости обусловлено шумом.
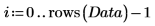
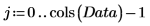
4. Используйте функцию mean, чтобы найти среднее значение данных, и затем вычитайте его из каждой переменной, чтобы центрировать данные.
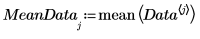
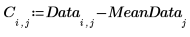
5. Постройте график центрированных данных.
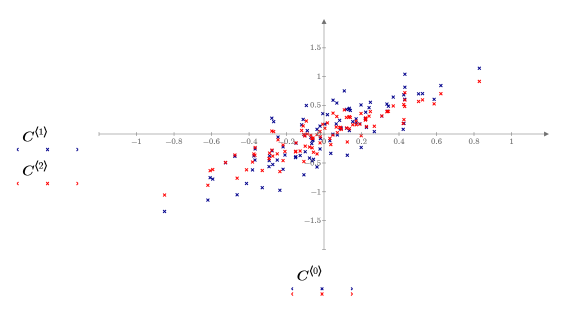
• Теперь данные расположены по центру относительно начала координат. Это одно из действий, которые функция Nipals выполняет автоматически. • Во многих применениях анализа PCA рекомендуется изменить масштаб данных таким образом, чтобы переменные имели равные веса (например, когда переменные имеют разные единицы измерения). Обычно применяется нормирование каждой переменной (каждого столбца данных) на единичную дисперсию. Для этих данных такой способ не подходит, поэтому нормирование не используется. |
6. Используйте функцию Nipals, чтобы создать новое пространство переменных. Используйте три главных компонента, что является максимально возможным количеством, поскольку есть только три начальные переменные.
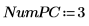
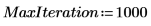
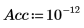
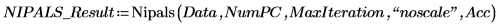
Выходными данными функции Nipals является вложенная матрица, состоящая из шести отдельных матриц. Используйте ее, чтобы найти значения loadings, scores, eigenvals и eigenvecs для данных. Если требуется, используйте функцию Nipals2 и последние две матрицы, чтобы извлечь дополнительные компоненты.
Нагрузки и количественные показатели
1. Вызовите функцию loadings для извлечения данных второй матрицы в матрице NIPALS_Result.
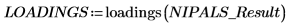
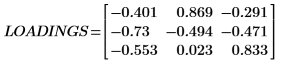
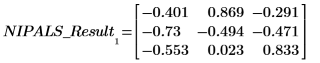
Каждый столбец LOADINGS представляет вектор нагрузки.
2. Вызовите функцию scores для извлечения данных первой матрицы в NIPALS_Result.
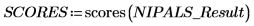

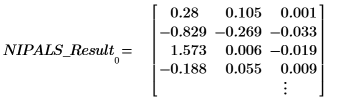
Количественные показатели представляют собой доли, с которыми суммируются векторы нагрузки для восстановления исходного спектра. Рассматривайте их как интенсивности. Data = LOADINGS * SCOREST.
3. Постройте график данных, сохраненных в матрице SCORES.
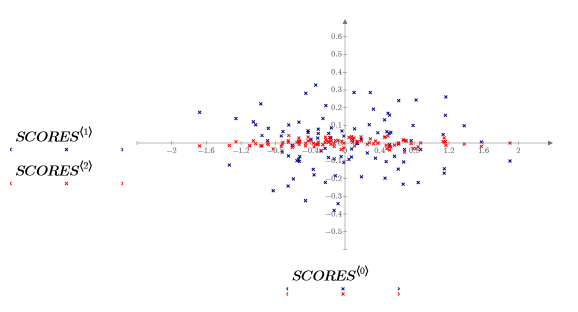
Данные были повернуты так, чтобы максимальная величина дисперсии могла быть объяснена первой переменной. На графике это представлено длинной осью эллиптического облака, которая теперь параллельна оси x. Значения третьей переменной, параллельной оси z, очень малы. В большинстве случаев эту переменную можно отбросить. Данные теперь сжаты.
Дисперсия PCA и собственные значения
1. Используйте функцию PCAvariance для возврата кумулятивных дисперсий трех главных компонентов.
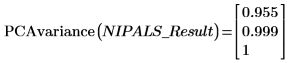
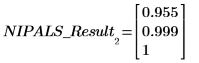
На первые два компонента приходится 99.9 % дисперсии в системе.
2. Используйте функцию PCAeigenvals для извлечения собственных значений главных компонентов.