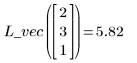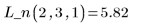Пример. Кусочно-квадратичная подгонка
Одномерная полиномиальная регрессия
Функция loess используется для аппроксимации данных квадратичными функциями с использованием локальной регрессии.
1. Определите следующую матрицу:

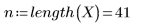
2. Определите диапазон - процентную долю общего числа точек в окне взвешивания вокруг каждой точки данных, используемую для последовательной квадратичной аппроксимации с помощью функции loess.
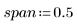
Общая рекомендация: значение (span*n) должно быть больше 1, так как число точек, по которым выполняется усреднение для каждой аппроксимации по методу наименьших квадратов, должно быть больше 1:
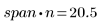
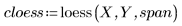
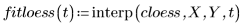
4. Вызовите функцию polyfit для аппроксимации набора данных полиномом второго порядка.
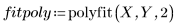
5. Постройте график двух кривых, определенных выше.
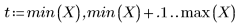
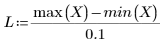
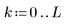
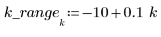
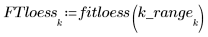
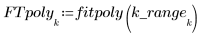
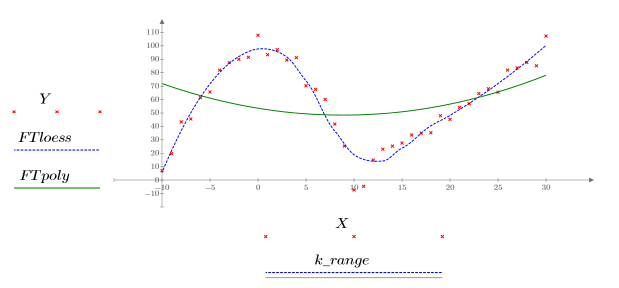
• В случае большого диапазона (например, 2 или 3) данные считаются единой квадратичной аппроксимацией с почти равными весами. Аппроксимация приближается к решению polyfit квадратного полинома.
• Дать точные рекомендации по выбору диапазона невозможно. С увеличением значения диапазона кривая аппроксимации loess становится более гладкой, поскольку в аппроксимации меньше элементов соединяются между собой. Однако полученная кривая может неудовлетворительно аппроксимировать данные. И наоборот, при уменьшении диапазона функция loess может не сходиться.
• Алгоритм loess не предназначен для экстраполяции. При попытке вычисления функции interp для значений, выходящих за пределы исходного диапазона x, возникает ошибка.
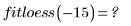
• Функцией loess можно воспользоваться, когда данные имеют в некоторой степени прерывистый характер, но не хочется выполнять кусочную подгонку вручную или использовать комплексные, физически нереалистичные или нелинейные методы аппроксимации.
Многомерная полиномиальная регрессия
Используйте функцию loess для расчета многомерной полиномиальной регрессии. Функция loess не может подбирать более четырех независимых переменных.
1. Задайте набор данных.
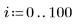
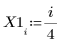
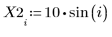
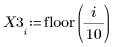
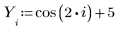
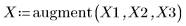
2. Задайте параметр сглаживания.
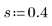
Этот параметр имеет такое же значение, как в однофакторном случае.
3. Вызовите функцию loess.
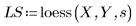
4. Вызовите функцию interp для интерполяции многомерных аппроксимирующих функций. Аппроксимирующая функция может принимать либо вектор, содержащий n элементов, либо набор из n аргументов, где n — число независимых факторов.
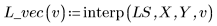
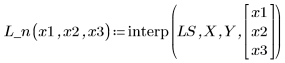
5. Используйте аппроксимирующие функции для прогнозирования значения Y в точке (2, 3, 1).