Пример. Нелинейная регрессия 2
Используйте функцию LeastSquaresFit для расчета нелинейной регрессии. Решатель LeastSquaresFit обладает наибольшей гибкостью при решении нелинейных задач регрессии. Он позволяет задавать уравнения ограничений для любых зависимых параметров, нижние и верхние границы параметров, среднеквадратические отклонения значений X, а также предел доверительного интервала для расчета.
LeastSquaresFit
1. Задайте набор данных.
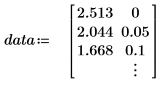
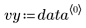
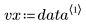
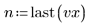
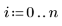
Данные берутся из примера, который обсуждался на веб-сайте NIST. Данные были сгенерированы с точностью до 14-го знака с помощью следующего уравнения:
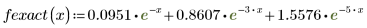
2. Задайте аппроксимирующую функцию.
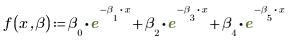
Отдельные параметры выше представляют элементы вектора β. Входную функцию также можно задать, используя имена отдельных переменных вместо элементов вектора:
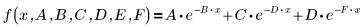
3. Задайте начальное приближение.
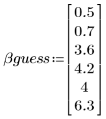
4. Задайте предел доверительного интервала для параметров.
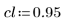
5. Вызовите функцию LeastSquaresFit.
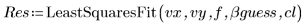
В решателе для решения задачи метода наименьших квадратов используется последовательное квадратичное программирование (SQP). Введение дополнительных переменных позволяет преобразовать исходную задачу в общую задачу нелинейного программирования с ограничениями в виде равенств, которая обычно решается быстрее и устойчивее по сравнению с другими методами.
6. Просмотрите выходной вектор, возвращенный функцией LeastSquaresFit.
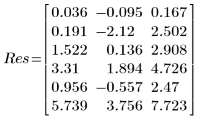
◦ Первый столбец вывода содержит значения параметров аппроксимации. Второй столбец содержит левую границу, а третий столбец — правую границу доверительного интервала для параметров.
◦ 95 % границ доверительного интервала для параметров охватывают достаточно большой диапазон, а это указывает на то, что выполнить аппроксимацию трудно, и параметры могут меняться в широких пределах. Как следствие, значения параметров аппроксимации отличаются от правильных значений, приведенных на веб-сайте NIST:
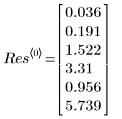

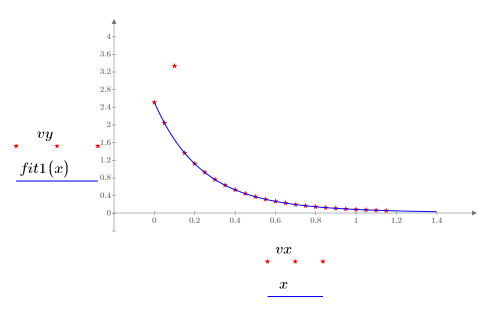
7. Постройте график данных, аппроксимацию по методу наименьших квадратов и аппроксимацию NIST.
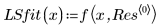
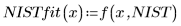
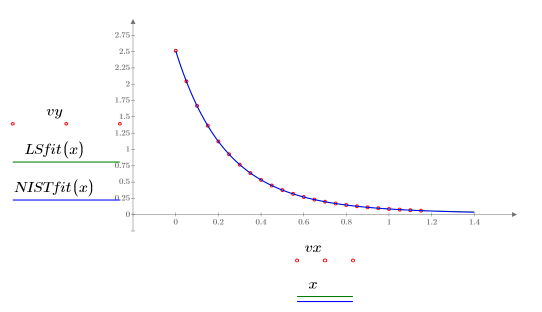
8. Сравните аппроксимацию по методу наименьших квадратов с исходными данными.
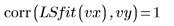
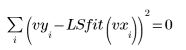
Аппроксимация приближается к сходимости, однако ее можно улучшить путем корректировки допуска сходимости. Это можно сделать с помощью одного из необязательных аргументов функции LeastSquaresFit.
Ограничения, среднеквадратическое отклонение и допуск
Для LeastSquaresFit имеется ряд необязательных аргументов:
• вектор среднеквадратического отклонения;
• матрица верхних и нижних границ;
• точность.
Необязательные аргументы можно использовать по отдельности, однако если введено несколько аргументов, имеет значение порядок их ввода.
1. Измените одно из значений данных для моделирования ошибки измерения.
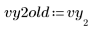
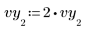
2. Задайте нижнюю и верхнюю границы для ограничения подобранных значений.
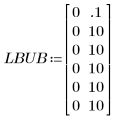
Заданные границы находятся за пределами диапазона ожидаемых значений параметров, поскольку в данном случае конкретные границы не известны.
3. Задайте вектор среднеквадратических отклонений для каждого значения y, чтобы скрыть отклонения.
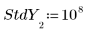
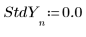
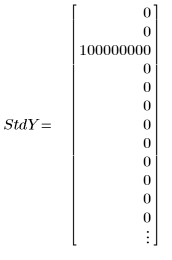
◦ Большое значение 108 среднеквадратического отклонения надежно удаляет ошибку измерения из расчета.
◦ Если вектор среднеквадратического отклонения вводится в виде аргумента функции LeastSquaresFit, решатель минимизирует следующую функцию:
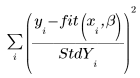
Если среднеквадратическое отклонение для точки равно 0, для этой точки используется исходная функция, т. е. StdYi равно 1.
4. Задайте точность для использования более строгого допуска сходимости расчета (значение по умолчанию 10-7).
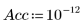
5. Вызовите функцию LeastSquaresFit с использованием и без использования среднеквадратического отклонения.
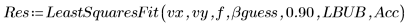
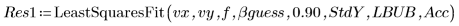
◦ Происходит сбой немаскированного расчета, поскольку границы доверительного интервала слишком большие.
◦ Новые значения параметров оказываются ближе к значениям NIST:
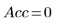
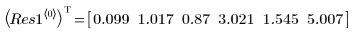
6. Постройте график данных с отклонением и замаскированной подгонкой.
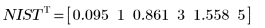
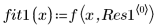
Справочная информация
Данные для этого примера взяты из книги C. Lanczos, Applied Analysis (Прикладной анализ), Prentice Hall, 1956, стр. 272–280, в том виде, в каком они содержатся в архиве наборов статистических справочных данных NIST