Пример. Модифицированные функции Бесселя второго рода
Покажите взаимосвязь между функциями K0, K1 и Kn. Также покажите взаимосвязи между этими функциями и их масштабированными версиями.
1. Определите две переменные определения шага:
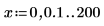
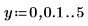
2. Постройте графики функций K0 и K1. Добавьте на график функцию второго порядка Kn:
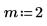
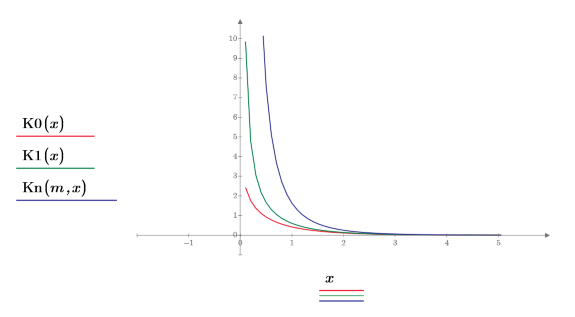
3. Постройте график функции Kn пятого и восьмого порядка:
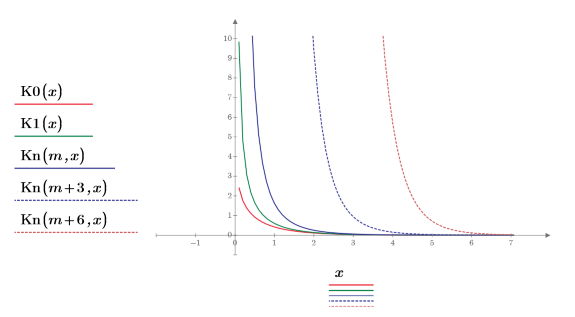
• Чем выше порядок функции Kn, тем больше функция сдвигается вправо. • Функции Kn любого порядка стремятся к бесконечности при x=0. |
4. Постройте график функции Kn с небольшой разницей в m, чтобы показать, что они стремятся к бесконечности с той же скоростью:
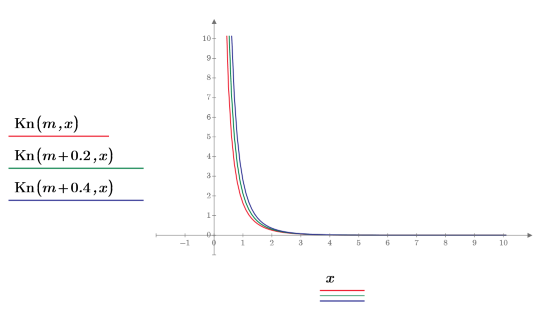
5. Создайте график, чтобы показать, что K0(y)=Kn(0,y). Сбросьте значения делений, чтобы увеличить масштаб по оси X и показать график более подробно:
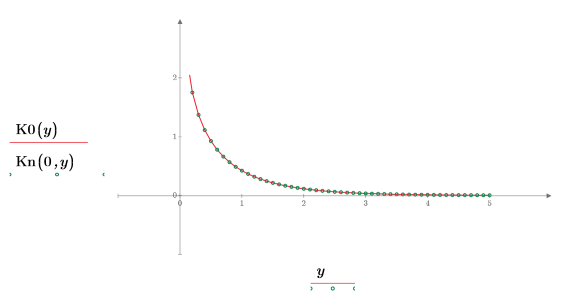
6. Создайте график, чтобы показать, что K1(y)=Kn(1,y). Сбросьте значения делений, чтобы увеличить масштаб по оси X и показать график более подробно:
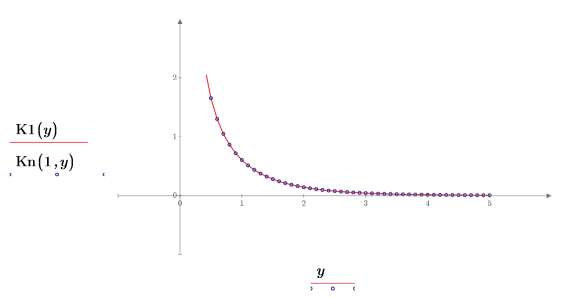
7. Используйте аналитические преобразования, чтобы показать взаимосвязь между каждой функцией и ее масштабированной версией:
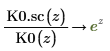
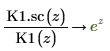
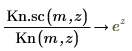
8. Создайте график, чтобы показать, что:
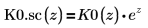
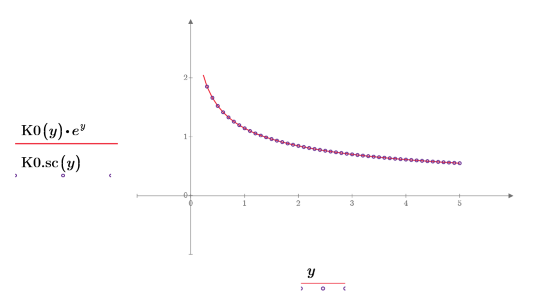
У модифицированных функций Бесселя второго рода нет пиков.