Пример. QR-разложение матрицы на множители
Используйте функцию QR, чтобы выполнить разложение на множители матрицы QR.
|
|
• Во избежание логических несоответствий при выполнении логических сравнений включите Приблизительное равенство (Approximate Equality) в выпадающем списке Параметры расчета (Calculation Options).
• В примере используется входная комплексная матрица, но функция также принимает на вход вещественную матрицу.
|
QR-разложение на множители с выбором главного элемента
1. Определите вещественную матрицу M1 размерности m x n так, что m > n.
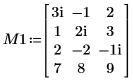
2. Задайте аргумент p, чтобы управлять включением и отключением выбора главного элемента.
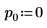
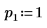
3. Используйте функцию QR, чтобы выполнить QR-разложение на множители матрицы M1.

Функция по умолчанию QR(M1) эквивалентна QR(M,1). 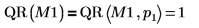 |
4. Покажите, что M1 x P1 = Q1 x R1.
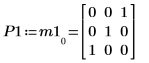


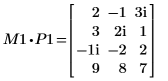 | 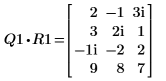 |
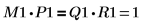 | |
Отношение логически истинно. | |
5. Используйте функцию submatrix, чтобы извлечь матрицу M2 так, чтобы m < n, а затем примените функцию QR.
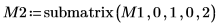
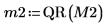
6. Покажите, что M2 x P2 = Q2 x R2.
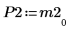 | 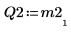 | 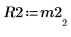 |
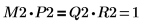 | ||
Отношение логически истинно. | ||
7. Используйте функцию submatrix, чтобы извлечь матрицу M3 так, что m = n, а затем примените функцию QR.
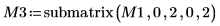
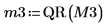
8. Покажите, что M3 x P3 = Q3 x R3.
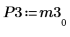 | 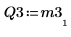 | 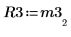 |
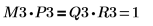 | ||
Отношение логически истинно. | ||
QR-разложение на множители без выбора главного элемента
1. Отключите выбор главного элемента, а затем примените функцию QR к матрице M1 (m > n).

2. Покажите, что M1 = Q10 x R10.


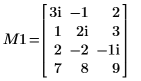 | 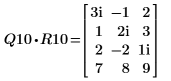 |
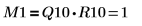 | |
Отношение логически истинно. | |
3. Отключите выбор главного элемента, а затем примените функцию QR к матрице M2 (m < n).
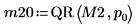
4. Покажите, что M2 = Q20 x R20.
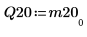 | 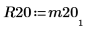 |
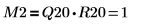 | |
Отношение логически истинно. | |
5. Отключите выбор главного элемента, а затем примените функцию QR к матрице M3 (m = n).
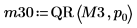
6. Покажите, что M3 = Q30 x R30.
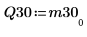 | 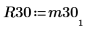 |
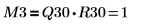 | |
Отношение логически истинно. | |