Пример. Методы линейного прогноза
Используйте функции burg и yulew, чтобы создать коэффициенты для названной модели линейного прогноза. В этих функциях применяется метод Бёрга и алгоритм Юла - Уолкера соответственно. Описание этих алгоритмов и их математическое обоснование см. в книге Optimum Signal Processing (Оптимальная обработка сигналов), Sophocles J. Orfanidis, Macmillan (1989).
Прогноз Юла-Уолкера
1. Используйте функцию cos, чтобы определить косинусоидальный сигнал.
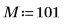
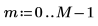
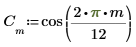
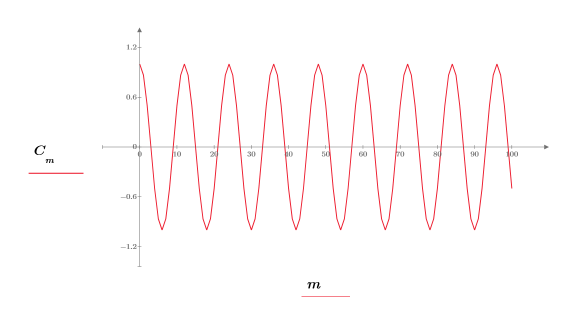
2. Постройте график сигнала.
3. Используйте функцию rnd, чтобы добавить случайный шум к сигналу.
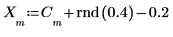
4. Постройте график исходного и зашумленного сигналов.
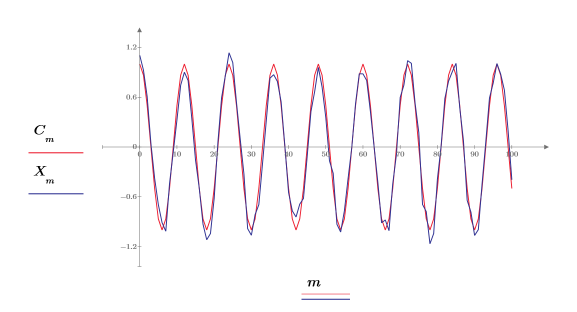
Из сигнала вычтено значение 0.2, чтобы центрировать случайный компонент вокруг нулевой амплитуды.
5. Сделайте короткую выборку из начальной части сигнала.
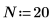
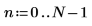
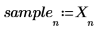
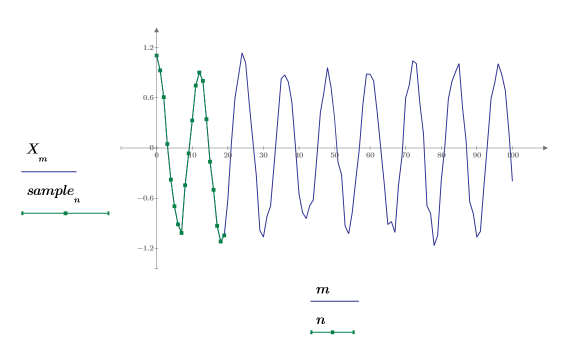
6. Установите порядок прогнозирования и используйте функцию yulew для вычисления коэффициентов.
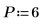
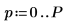

◦ Эти коэффициенты предназначены для полюсного фильтра, аппроксимирующего исходный сигнал. Как и ожидалось, фильтр имеет один большой полюс, представляющий косинус, и несколько полюсов поменьше, аппроксимирующих шум.
◦ Порядок P определяет количество последовательных значений, используемых для прогнозирования следующего значения в ряду. Используются элементы вектора коэффициента с первого по шестой, а нулевой элемент, всегда равный 1, игнорируется. Это значение 1 нужно, когда y используется как фильтр ошибки прогнозирования для создания полного набора ошибок прогноза.
7. Сравните прогнозируемые точки, рассчитанные с помощью предыдущих P точек в сигнале, с исходными данными. Это позволяет увидеть, насколько хорошо функционировал бы фильтр при использовании вместо сигнала X.
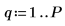
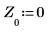
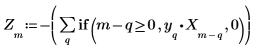
8. Постройте график исходного и спрогнозированного сигнала.
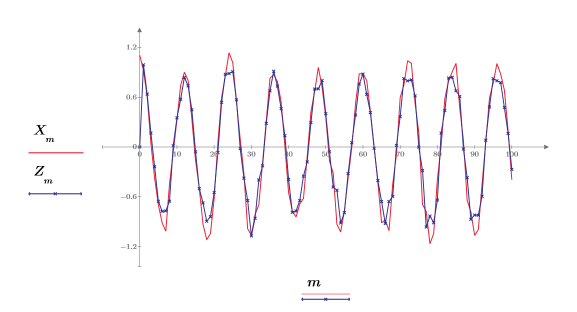
Получена очень хорошая аппроксимация, даже если использовать только первые 20 точек данных.
9. Используйте функцию response, чтобы генерировать ошибки прогнозирования для коэффициентов Юла - Уолкера, используя массив коэффициентов как фильтр, а затем вычисляя отклик с выборкой в качестве входных данных.
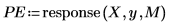
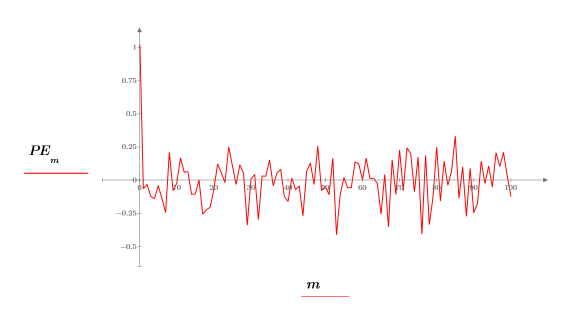
Полный массив коэффициентов иногда называют фильтром ошибки прогнозирования.
10. Убедитесь, что эти ошибки действительно дают разницу между двумя предыдущими графиками.
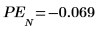
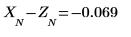
Алгоритм Юла - Уолкера минимизирует сумму квадратов ошибок прогнозирования.
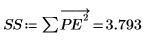
11. Выполните выборочную проверку минимизации, возмутив y (добавляя небольшое случайное значение ко всем коэффициентам, кроме первого) и заново вычислив сумму (поместите курсор на функцию rnd ниже и нажмите клавишу [F5] несколько раз).
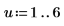
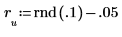
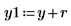
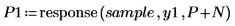
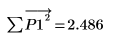
Прогноз Бёрга
1. Постройте последовательность, для которой хорошо работает линейный прогноз: авторегрессионный процесс с известными коэффициентами.
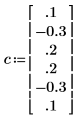
2. Инициализируйте временной ряд.
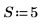
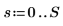
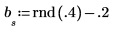
3. Создайте остальную часть ряда, используя сумму авторегрессии и шума.
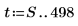
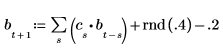
4. Возьмите целый временной ряд в качестве выборки и вычислите коэффициенты для модели порядка 6, а затем используйте функцию burg для вычисления коэффициентов.
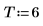
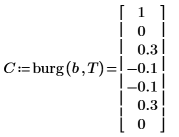
5. Сравните коэффициенты, фактически создавшие процесс, с помощью правила знаков для данного документа.
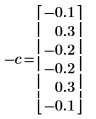
◦ Нулевой коэффициент не был учтен, так как он всегда равен единице.
◦ Вычисленные элементы 1 и 5 для C различаются.
6. Используйте вектор коэффициента Бёрга C, чтобы создать ошибки прогнозирования.
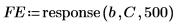
◦ Метод Бёрга назначает нулевой вес первым P ошибкам, так что минимизация не затрагивается заполнением выборки нулями, как это происходит в случае минимизации с помощью алгоритма Юла - Уолкера.
◦ Критерий Бёрга также использует как прямые ошибки FE, так и обратные ошибки BE.
7. Используйте функции response и reverse для вычисления обратных ошибок.
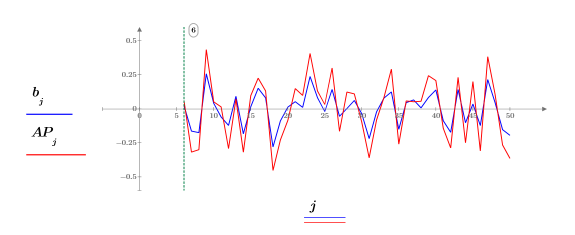
8. Используйте ошибки прогнозирования FE и функцию авторегрессии b для вычисления актуальных прогнозов AP, а затем отобразите на графике участок прогнозируемого и фактического рядов, начиная с элемента Pth.
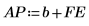
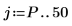
Спектральный анализ
Можно использовать коэффициенты, созданные при помощи методов линейного прогноза, для оценки спектра мощности моделируемого процесса. В этом контексте алгоритм Бёрга известен как система спектрального анализа максимальной энтропии (MESA), и в некоторых случаях он может определять спектры коротких временных рядов более точно, чем FFT.
Оцените спектр мощности процесса, представляющего собой сумму синусоид с добавлением гауссова шума.
1. Используйте функцию sin для определения сигнала с двумя синусоидальными компонентами.
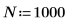
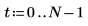
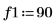
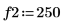
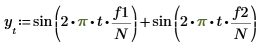
2. Используйте функцию gaussn для добавления гауссова шума.
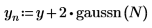
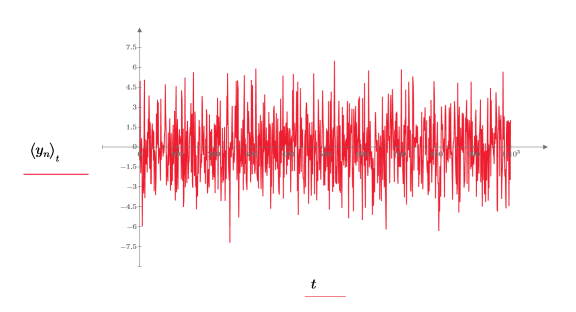
Функция gaussn возвращает n-мерный вектор случайных чисел, следуя гауссову распределению вероятностей со средним, равным 0, и среднеквадратическим отклонением, равным 1.
3. Определите два порядка для линейного прогнозирования.
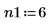
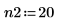
4. С помощью функции burg оцените спектр с авторегрессивными моделями двух порядков, используя в качестве выборки полную временную последовательность.
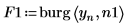
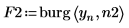
5. Используйте функцию gain, чтобы рассчитать соответствующие спектры мощности как квадратную величину амплитуды функции преобразования, определенной с помощью массивов коэффициентов F1 и F2.
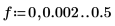
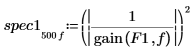
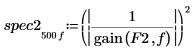
6. Постройте график двух спектров мощности.
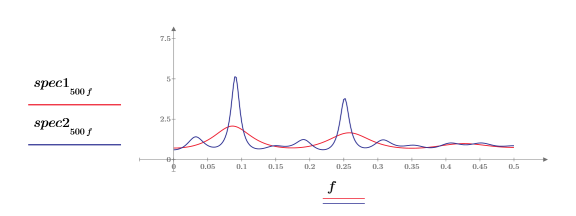
◦ Каждый спектр мощности имеет два пика.
◦ Нижние и верхние пики частоты для обоих спектров возникают примерно на одной частоте.
7. Разделите каждую из кривых spec1 и spec2 на два сегмента, чтобы упростить поиск пиков приращения и частот, на которых они возникают.
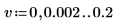 | 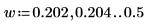 |
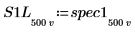 | 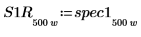 |
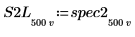 | 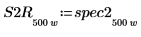 |
8. Используйте функцию if, чтобы определить функцию, возвращающую частоту, на которой данный сегмент имеет пик, а затем используйте ее для поиска левых и правых пиков каждой кривой спектра.
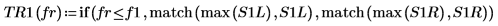 | |
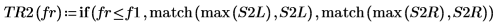 | |
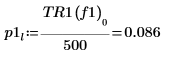 | 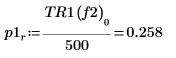 |
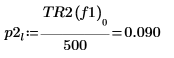 | 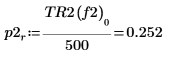 |
9. Используйте функцию max для вычисления величины каждого пика.
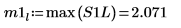 | 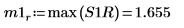 |
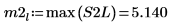 | 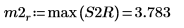 |
10. Постройте график каждой функции отдельно. Используйте горизонтальные и вертикальные маркеры, чтобы показать величину каждого пика и частоту, на которой он возникает.
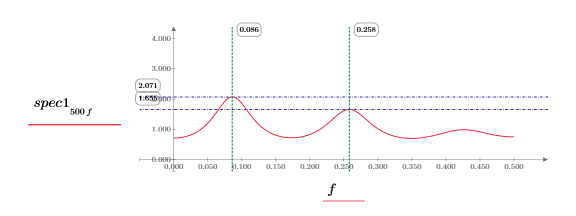
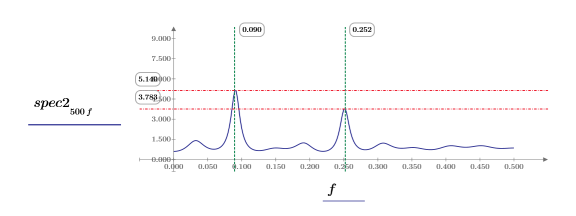
◦ Следите за двумя графиками при перерасчете документа.
◦ Величина пиков изменяется при каждом перерасчете и они, как правило, имеют разные значения. Возможно, однако, что величины будут равными.
◦ Пики возникают приблизительно на одних частотах.
Дополнительные сведения об этом методе спектральной оценки см. в книге Digital Spectral Analysis with Applications, написанной S. Lawrence Marple, Jr.