Пример. Сплайн по наименьшим квадратам
Spline2, Binterp и DWS
Используйте функцию Spline2, чтобы найти оптимальный набор узлов, необходимый функции Binterp для вычисления сплайновой интерполяции наименьших квадратов.
1. Задайте набор данных.

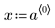 | 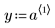 | 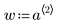 |
w является вектором весов, дающим предположительные стандартные отклонения случайной ошибки в y.
2. Определите степень желаемых сплайновых многочленов.
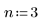
3. Вызовите функцию Spline2.
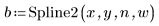

Первый элемент вектора b является порядком B-сплайна. Второй элемент дает количество интервалов (knots - 1). Следующие элементы представляют значения узлов. Остальные элементы содержат коэффициенты для базисных функций B-сплайна.
Первый и последний узлы при автоматической их генерации соответствуют конечным точкам исходных x-данных:
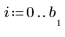
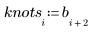
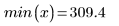 | 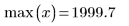 |
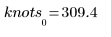 | 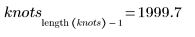 |
4. Вызовите функцию Binterp для получения диапазона значений, соответствующего диапазону x.
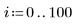
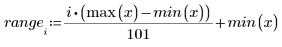

Строка i переменной spline1 содержит значение, полученное интерполяцией, а также вторую и третью производные в точке, определенной на интервале i.
5. Распечатайте исходные данные и интерполированный сплайн.
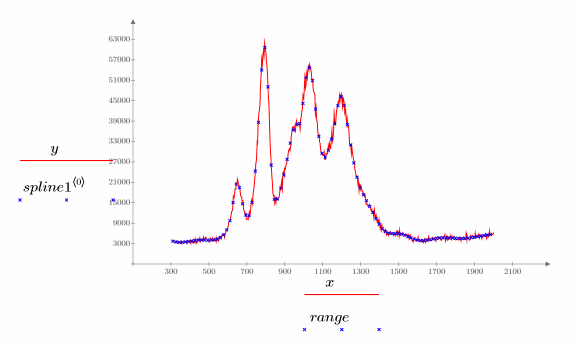
Оптимальное количество узлов и расстояние между ними определяются с помощью статистического показателя Дурбина-Уотсона. Для хорошего соответствия этот показатель должен быть близок к 2. Показатель может быть найден с помощью функции DWS или через извлечение подходящего элемента из матрицы b:
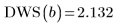
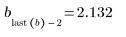
6. Используйте необязательный последний аргумент функции Spline2, долю от 0 до 1, чтобы получить уровень значимости или уровень браковки для критерия Дурбина-Уотсона.
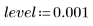
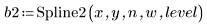
Как правило, хотя и не всегда, более высокие уровни браковки дают больше узлов и требуют более долгих расчетов.
7. Рассчитайте количество узлов, используемых функцией Spline2.
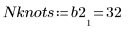
8. Вызовите функцию DWS для расчета статистического показателя Дурбина-Уотсона.
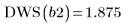
9. Распечатайте два интерполированных сплайна.
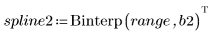
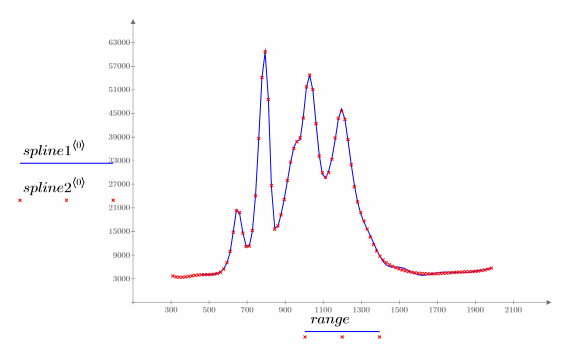
Можно интерполировать без весов:
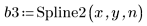
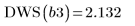
Можно интерполировать без весов, но с уровнем браковки:
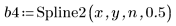
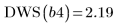
Производные сплайна
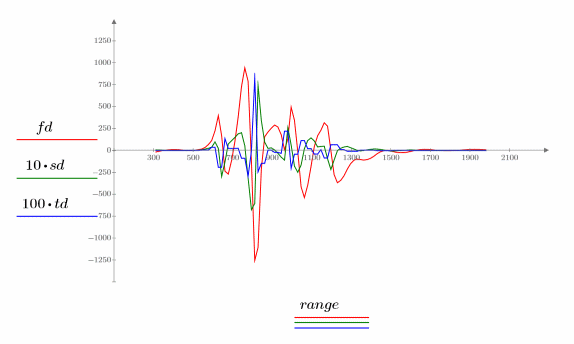
Распечатайте первые три производные сплайна интерполяции.
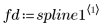
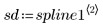
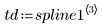
Использование собственных узлов
Можно использовать собственные узлы для интерполяции B-сплайном.
1. Определите строку узлов.
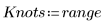
2. Распечатайте интерполированный сплайн.
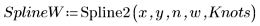
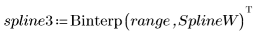
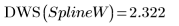
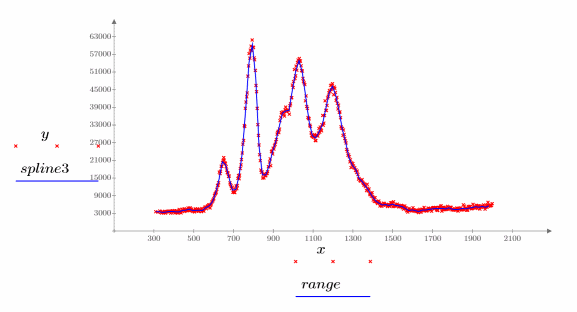
Можно использовать узлы без весового вектора:

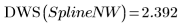
Отклонения
Можно увидеть эффект, оказываемый удалением отклонения на сплайновую интерполяцию.
1. Вызовите функцию GrubbsClassic, чтобы обнаружить точку, наиболее вероятно являющуюся отклонением.

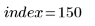
На самом верху второго пика данных есть подозрительная точка.
2. Удалите эту точку из набора данных и из весовой функции.
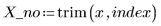
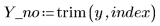
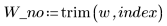
3. Вызовите функцию Spline2 для нового набора данных.
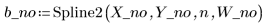
Согласно статистическому показателю Дурбина-Уотсона, соответствие улучшилось:
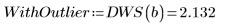
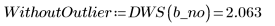
4. Сравните результаты интерполяций при подозрительном значении данных:
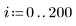
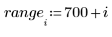
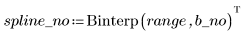
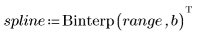
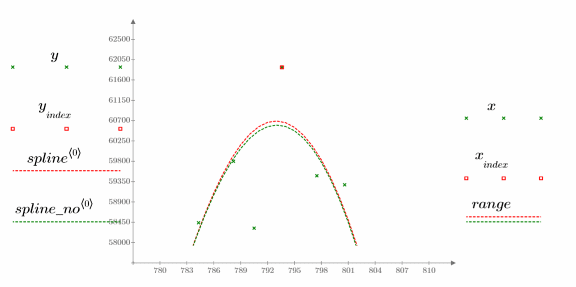
Сплайн немного падает при удалении отклонения.