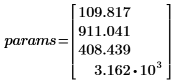Пример. Оператор градиента
• Определите функцию f:
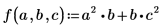
Используйте оператор градиента, чтобы получить вектор частных производных для f:
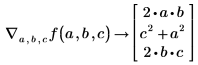
• Определите векторную функцию и рассчитайте градиент функции f по вектору x.
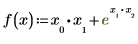

В этом примере для переменной ORIGIN, которая задает начальный индекс для всех массивов, задано значение 0.
Переменной с наибольшим нижним индексом в fявляется x2. Mathcad [подразумевает]предполагается, что имеются три переменные: x0, x1 и x2. В результате получаем вектор градиента из трех значений, содержащий частные производные этих переменных. Если x0 или x1 не отображаются в f, Mathcad по-прежнему возвращает вектор из трех значений, но элементы, соответствующие отсутствующим переменным, задаются равными 0.
Для наибольшего нижнего индекса, отображаемого в f, n, Mathcad подразумевает n + 1 переменных, x0, x1, ... xn, и возвращает вектор длины n + 1.
• При численном определении x можно рассчитать градиент со знаком равенства =. Mathcad рассчитывает градиент для значений x и возвращает вектор из чисел, представляющий градиент в точке x. Длина x должна быть больше наибольшего нижнего индекса, отображаемого в f, и Mathcad возвращает градиент с записями length(x).
В следующем примере x0 и x1 являются единственными переменными, появляющимися в выражении; Mathcad берет частные производные по x0 и x1 возвращает вектор из двух значений.
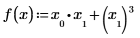
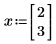
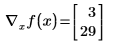
Однако при определении x как вектора из трех элементов Mathcad предполагает, что существует дополнительная переменная x2, которая не появляется в выражении. Результатом является вектор из трех элементов.
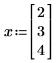
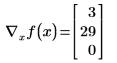
Использование оператора градиента с функцией genfit
Оператор градиента особенно удобен для настройки аргументов функции genfit, которая сопоставляет набору данных общую нелинейную функцию.
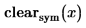
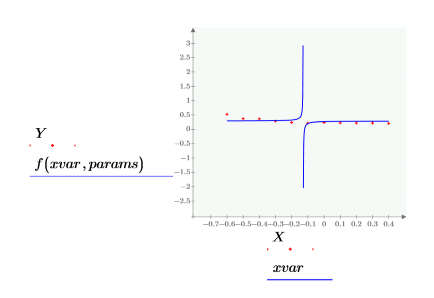
• Используйте данные из следующей таблицы.
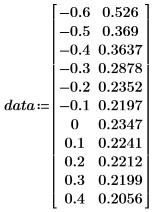
• Первый столбец содержит значения x данных, а второй - значения y.
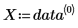
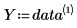
• Моделируем данные с помощью функции следующего вида:
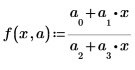
Где a1, a2 и a3 - неизвестные параметры, содержащиеся в векторе a.
Для моделирования данные можно вызвать genfit следующим образом:
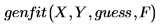
В этом выражении
◦ X и Y являются векторами, содержащими значения данных x и y.
◦ guess - вектор значений начального приближения для параметров.
◦ F - вектор, первым элементом которого является моделирующая функция f(x, a), а остальные элементы представляют частные производные по неизвестным параметрам f.
• Создайте вектор F, используя оператор градиента и функцию stack.
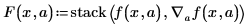

• Функция stack помещает моделирующую функцию f над вектором частных производных, созданным оператором градиента.
• Затем создайте вектор начального приближения для параметров.
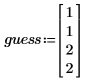
• Примените genfit следующим образом:
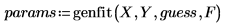
• Параметры, которые дают наилучшее приближение: