Пример. Основные операции со строками в матрицах
Выполните основные строковые операции трех типов в матрице m x n и покажите, что существует связь с приведенно-ступенчатой формой по строкам.
1. Задайте входную матрицу:
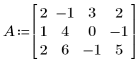
2. Умножьте строку r на скаляр c:
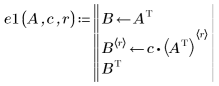
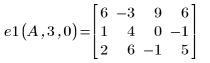
3. Замените строку r на сумму строки r и умноженной на c строки s:
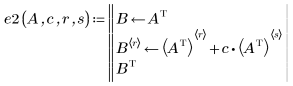
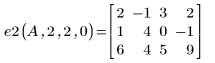
4. Поменяйте местами строки r и s:
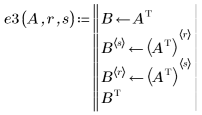
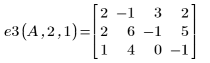
Приведенно-ступенчатая форма по строкам (rref) для матрицы
Приведенно-ступенчатая форма по строкам применяется при решении систем линейных уравнений.
Используйте следующую последовательность операций e1, e2 и e3 для получения приведенно-ступенчатой формы по строкам (rref) матрицы A:
1. Задайте матрицу A.
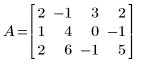
2. Используйте операцию e2, чтобы заменить строку 0 матрицы A на сумму строки 0 и умноженной на (-2) строки 1.
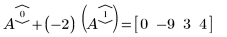
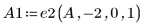
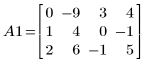
3. Используйте операцию e2, чтобы заменить строку 2 матрицы A1 на сумму строки 2 и умноженной на (-2) строки 1.
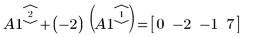
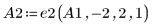
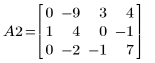
4. Используйте операцию e1, чтобы умножить строку 2 матрицы A2 на (-1/2).
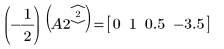
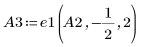
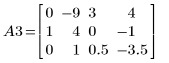
5. Используйте операцию e2, чтобы заменить строку 1 матрицы A3 на сумму строки 1 и умноженной на (-4) строки 2.
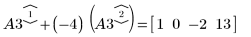
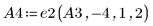
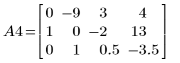
6. Используйте операцию e2, чтобы заменить строку 0 матрицы A4 на сумму строки 0 и умноженной на (9) строки 2.
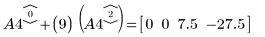
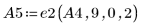
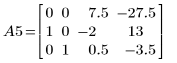
7. Используйте операцию e1, чтобы умножить строку 0 матрицы A5 на 2/15.
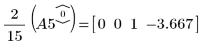
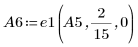
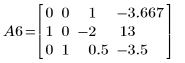
8. Используйте операцию e2, чтобы заменить строку 1 матрицы A6 на сумму строки 1 и умноженной на (2) строки 0.
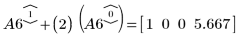
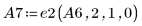
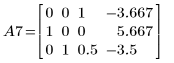
9. Используйте операцию e2, чтобы заменить строку 2 матрицы A7 на сумму строки 2 и умноженной на (-1/2) строки 0.
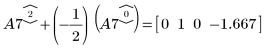
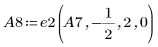
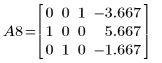
10. Используйте операцию e3, чтобы поменять местами строки 0 и 1 матрицы A8.
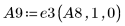
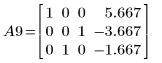
11. Используйте операцию e3, чтобы поменять местами строки 1 и 2 матрицы A9.
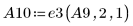
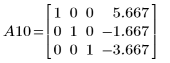
В этом примере описанная последовательность основных операций со строками позволяет получить приведенно-ступенчатую форму по строкам матрицы A.
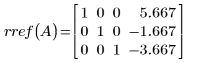
Возвращенная функцией матрица совпадает с матрицей A10.