Пример. Собственные векторы и собственные значения
Используйте функции eigenvals, eigenvecs и eigenvec, чтобы найти собственные значения и собственные векторы действительной или комплексной матрицы. Проверьте теорию, согласно которой для квадратной матрицы M ненулевой вектор v является собственным вектором M, если можно найти такое число λ, для которого:
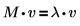
1. Определите квадратную матрицу ввода.
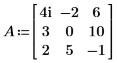
2. Вызовите eigenvals и eigenvecs, чтобы найти собственные значения и собственные векторы матрицы A.
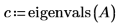
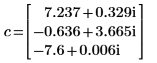
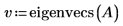

Первый столбец v представляет собой собственный вектор, соответствующий первому элементу c. Аналогично второй столбец v является собственным вектором, соответствующим второму элементу c, и т. д.
3. Задайте v1 в качестве первого собственного вектора и c1 в качестве первого собственного значения A. Сравните A x v1 с c1 x v1.
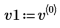
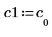
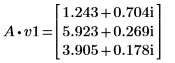 | 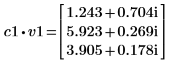 |
4. Задайте v2 в качестве первого собственного вектора и c2 в качестве первого собственного значения A. Сравните A x v2 с c2 x v2.
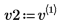
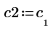
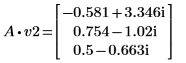 | 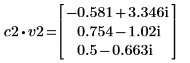 |
5. Задайте v3 в качестве первого собственного вектора и c3 в качестве первого собственного значения A. Сравните A x v3 с c3 x v3.
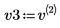
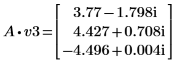 | 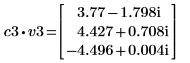 |
6. Вызовите функцию eigenvec, чтобы вернуть один собственный вектор для определенного собственного значения.
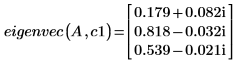

Результаты, возвращенные eigenvec и eigenvecs, не обязательно совпадают, но тем не менее являются верными решениями. Собственный вектор не является уникальным. Он связан с другими собственными векторами при помощи коэффициента масштабирования. Для данного собственного значения существует бесконечное число собственных векторов.