Пример. Дискретное косинусное преобразование

Функции > Обработка изображений > Область преобразования > Пример. Дискретное косинусное преобразование

Используйте функции dct и idct, чтобы рассчитать дискретное косинус-преобразование и обратное преобразование соответственно. Данное преобразование имеет преимущество, поскольку концентрирует большую часть "энергии" (информации) изображения в нескольких частотных составляющих.

Сведения об использовании этого примера см. в разделе Сведения о примерах обработки изображений.

1. Определите матрицу M с размером N x P.

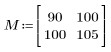
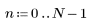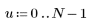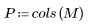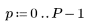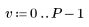2. Реализация косинусного преобразования использует тип II DCT. Определите DCT для аналитической формулы этого преобразования.

Щелкните для копирования этого выражения

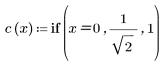
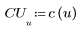
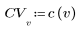
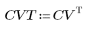
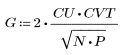
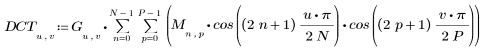
3. Вычислите матрицу DCT.

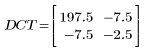
4. Примените функцию dct к матрице M.

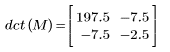
5. Вычислите максимальную ошибку между DCT и функцией dct.

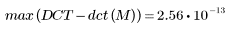
Сравнение энергии

У косинусного преобразования очень хорошие свойства сжатия: большая часть энергии концентрируется в первых нескольких коэффициентах преобразования.

1. Определите входную матрицу.

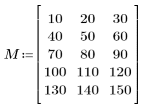
2. Примените функцию dct к матрице M и вычислите ее.

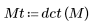
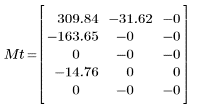
Результирующая матрица показывает, что большая часть энергии, которая относится к значениям коэффициентов, сконцентрирована в нескольких первых элементах.

idct

Обратная функция используется для восстановления исходного изображения из его преобразования.

1. Прочтите в черно-белой версии Мону Лизу.

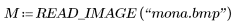
(mona.bmp)

2. Примените функцию dct, чтобы преобразовать изображение.

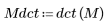
(mona_noise.bmp)

3. Примените обратную функцию, чтобы восстановить изображение.

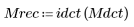
(mona_rec.bmp)

4. Проверьте свойство cжатия энергии DCT, просмотрев гистограммы преобразованных и исходных изображений.

<region id="ID0EZBIZ" top="3000" left="24" width="597" height="312" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace>
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">k_range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">H</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">Horig</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

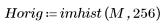
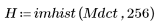
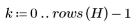
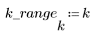
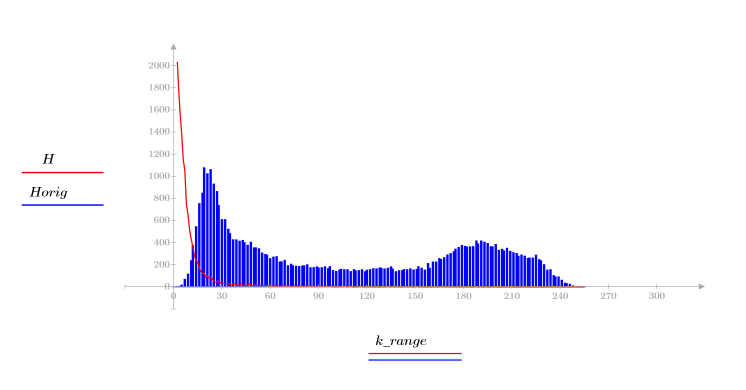
Преобразованное изображение концентрирует большую часть энергии в первых нескольких столбцах гистограммы, пока происходит распределение исходного изображения. Благодаря этому преобразованное изображение — оптимальный выбор для кодировки символов или передачи, поскольку большая часть информации изображения может быть передано с очень малым числом частотных компонентов. Именно поэтому для сжатия изображений используется DCT.

Похожие темы

Дискретное косинусное преобразование

1D- и 2D-гистограммы

Было ли это полезно?