Пример: Сочетания и перестановки
Используйте функции combin и permut, чтобы посчитать поднаборы элементов. Порядок элементов является существенным в перестановках, но не в сочетаниях.
1. Задайте количество элементов и количество элементов в каждом поднаборе:
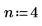
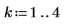
2. Примените функцию combin, чтобы вычислить количество сочетаний:
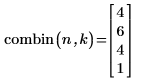
При работе с четырьмя элементами есть четыре способа группировать элементы по одному, шесть способов группировать элементы по два, четыре способа группировать элементы по три и один способ группировать элементы по четыре.
3. Предположим, имеются буквы A, B, C и D. Перечислим четыре сочетания по одной букве в наборе:
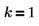 | A, B, C, D |
4. Перечислим шесть сочетаний по две буквы в наборе:
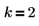 | AB, AC, AD, BC, BD, CD |
Наборы BA, CA, DA, CB, DB, DC содержат те же буквы, что и наборы AB, AC и т. д., поэтому не считаются разными сочетаниями.
5. Примените функцию permut, чтобы вычислить число перестановок:
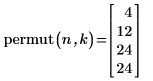
6. Перечислим 16 перестановок по две буквы в наборе:
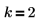 | AB, AC, AD, BC, BD, CD |
BA, CA, DA, CB, DB, DC |
Наборы AB и BA считаются другими перестановками наборов A и B.
7. Перечислим 24 перестановки по три буквы в наборе:
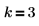 | ABC, ACB, ABD, ADB, ACD, ADC |
BAC, BCA, BAD, BDA, BCD, BDC | |
CAB, CBA, CAD, CDA, CBD, CDB | |
DAB, DBA, DBC, DCB, DAC, DCA |