Пример. Функции Бесселя
Использование сферической функции Бесселя и сферической функции Ганкеля для поиска решений уравнения Шредингера в трехмерной прямоугольной потенциальной яме (атоме).
Решение представляет разрешенные значения энергии, при которых внутренняя и внешняя волновые функции принимают одинаковые значения и первые производные. Эти значения энергии существуют для всех значений момента количества движения (l).
1. Задайте массу, постоянную Планка и радиус ядра:
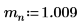
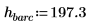
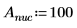
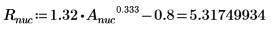
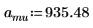
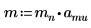
2. Задайте нулевое значение момента количества движения:
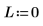
3. Задайте потенциальную энергию ямы и постройте ее график:
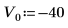
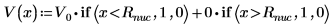
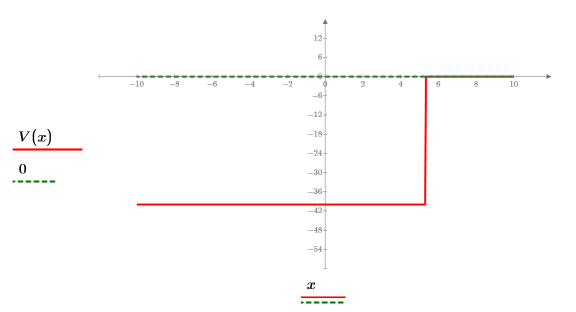
4. Используйте сферические функции Бесселя и сферические функции Ганкеля для поиска решений:
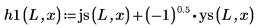
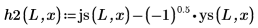
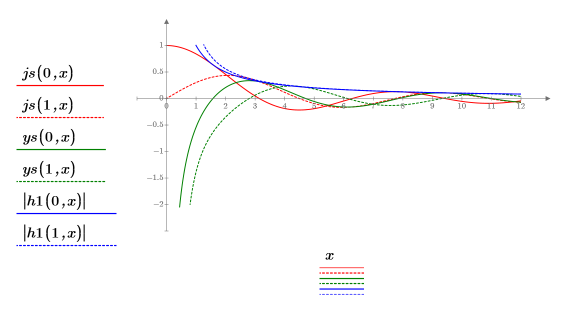
5. Задайте для граничных состояний E < 0 волновые функции для решения по первому энергетическому состоянию внутри и снаружи потенциальной ямы:
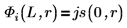
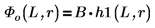
B представляет относительную нормализацию.
6. Задайте постоянные распространения:
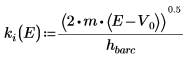
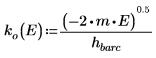
Аргумент решения за пределами потенциальной ямы является мнимым, поскольку волна за пределами ямы затухает.
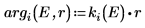
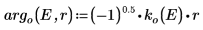
7. Совместите волновые функции на краю потенциальной ямы (радиус ядра), чтобы определить относительную нормализацию:
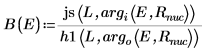
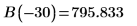
8. Совместите производные. Определите собственные значения, отыскав точки, где производные равны.
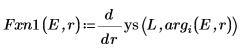
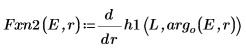
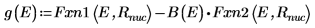
9. Предоставьте два начальных приближения для E:
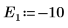
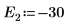
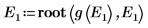
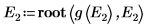
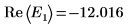
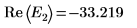
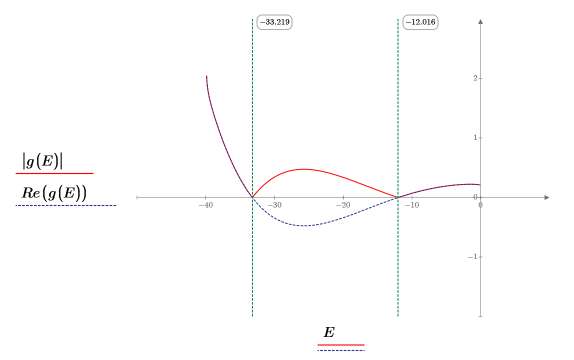
10. Постройте график зависимости g(E) от E и добавьте вертикальные маркеры, чтобы показать две корневые точки: