Пример. ANOVA для нереплицируемых факториалов
Используйте функцию anova, чтобы выполнить анализ дисперсии для факторного эксперимента без репликации путем обнаружения незначительного фактора и проецирования факториала в факториал младшего порядка.
1. Вызовите функцию fullfact, чтобы построить матрицу полного факторного плана для эксперимента, тестирующего скорость фильтрации опытной установки. Факторы A, B, C и D отвечают за температуру, давление, концентрацию формальдегида и скорость перемешивания соответственно.
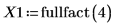
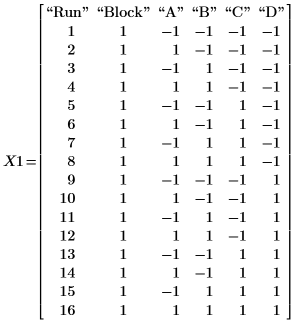
2. Запишите результаты эксперимента в матрице Y1 с одним элементом для каждого из шестнадцати выполнений.

3. Вызовите функцию quickscreen, чтобы получить средний отклик для каждого основного фактора.

4. Создайте диаграмму распределения, чтобы определить значимые факторы.
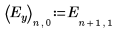
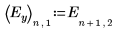

Фактор C и взаимодействия второго порядка, использующие фактор C, слабо влияют на эксперимент. В сравнении с факторами A, B и D фактор C не является значимым.
5. Используйте функцию anova, чтобы выполнить анализ дисперсии.
Функция anova вернет ошибку, поскольку матрица Y1 не имет репликаций. Тем не менее, так как C не является значимым, выполнения “Run 1” и "Run 5" дублируются, поскольку факторы A, B и D ограничены. Это также справедливо и для выполнений “Run 2" и "Run 6". Фактически вся матрица плана ABCD 24 содержит дубликат матрицы плана ABD 23, если фактор C не является значимым.
6. Используйте функцию fullfact, чтобы создать полнофакторную матрицу плана 23.

В матрице X2 имена факторов будут изменены. Первоначальные обозначения факторов A, B, D изменятся на A, B, C.
7. Переставьте результаты эксперимента для достижения соответствия полнофакторному эксперименту 23.
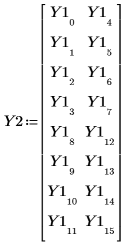
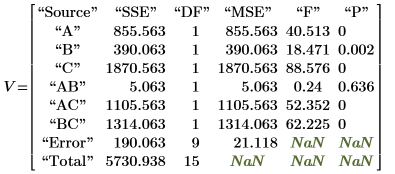
8. Вызовите функцию anova, используя Y2.
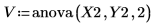
9. Используйте функцию qF, чтобы вычислить критическое значение F-value для факторов и взаимодействий и сравнить их F-value с критическим F-value.
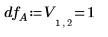
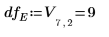
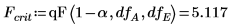
◦ Диаграмма распределения показывает, что фактор C не является значимым в сравнении с A, B и D.
◦ Факторы A, B, D (отображенные в V как A, B, C) и их взаимодействия AD, BD (отображенные в V как AC, BC) являются значимыми на уровне 5 %, поскольку их F-values больше, чем Fcrit. Данный анализ дисперсии лишь усиливает субъективное заключение, полученное из диаграммы распределения.
Справочная информация
Montgomery, D.C., Design and Analysis of Experiments (Планирование и анализ эксперимента) (на англ. яз.), 5th ed., John Wiley & Sons, New York, 2001, стр. 246.