Esempio: solutore statespace

Funzioni > Soluzione e ottimizzazione > Solutori di equazioni differenziali > Esempio: solutore statespace

Utilizzare il solutore statespace per risolvere una rappresentazione statespace di un sistema di equazioni differenziali ordinarie (ODE) di primo ordine.

In particolare, trovare la soluzione al caso di un oscillatore armonico smorzato in cui il lato destro dell'equazione dell'oscillazione armonica è 0:

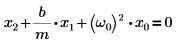
Esistono quattro casi per la soluzione: sovrasmorzata, smorzata criticamente, sottosmorzata e feedback stato completo.

Soluzione sovrasmorzata

1. Scrivere l'equazione matematica per la soluzione sovrasmorzata:

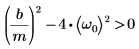
2. Definire le condizioni iniziali, la massa dell'oggetto, la costante di smorzamento, l'inizio e la fine dell'intervallo di integrazione e il numero di punti:

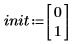
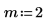
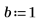
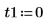
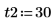
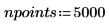
3. Impostare la frequenza naturale, o risonante, del sistema.

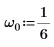
4. Verificare la presenza della condizione di sovrasmorzamento:

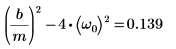
5. Scrivere l'equazione ODE in forma di matrice:

Fare clic per copiare questa espressione

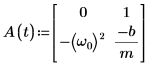
6. Chiamare la funzione statespace:

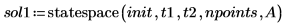
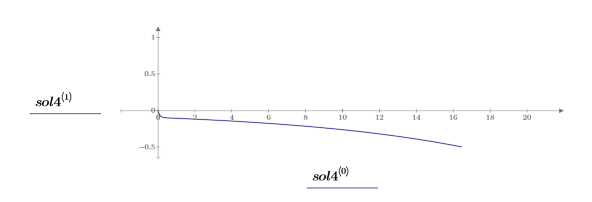
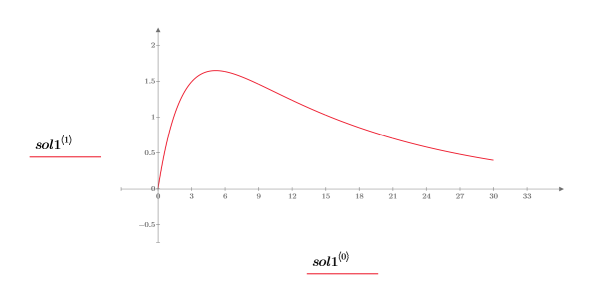
7. Tracciare il grafico della soluzione:

<region id="ID0ESY25" actualWidth="591.8" actualHeight="288" top="940.80000000000018" left="19.200000000000003" height="288" width="591.8" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="56">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="457.4" height="230.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="33">
          <axisLine position="origin" positionticmark="1" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol1</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol1</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="57">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="58">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Soluzione smorzata criticamente

1. Impostare la frequenza naturale, o risonante, del sistema.

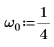
2. Verificare la presenza della condizione di smorzamento critico:

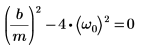
3. Scrivere l'equazione ODE in forma di matrice:

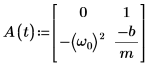
4. Chiamare la funzione statespace:

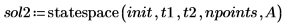
5. Tracciare il grafico della soluzione:

<region id="ID0ETA35" actualWidth="590.8" actualHeight="288" top="1728.0000000000002" left="19.200000000000003" height="288" width="590.8" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="63">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="456.4" height="230.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="33">
          <axisLine position="origin" positionticmark="1" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol2</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol2</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="64">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="65">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue resultRef="66">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

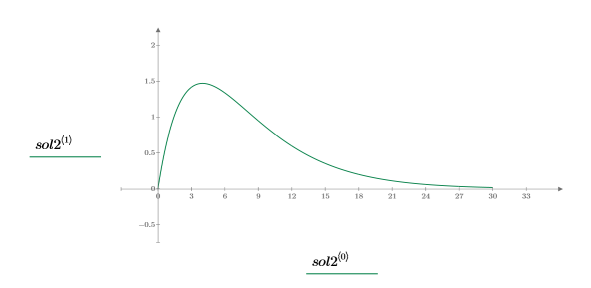
Soluzione sottosmorzata

1. Impostare la frequenza naturale, o risonante, del sistema.

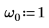
2. Verificare la presenza della condizione di sottosmorzamento

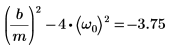
3. Scrivere l'equazione ODE in forma di matrice:

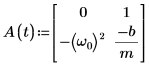
4. Chiamare la funzione statespace:

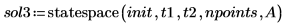
5. Tracciare il grafico della soluzione:

<region id="ID0EUI35" actualWidth="591.6000126600261" actualHeight="201.60000429153402" top="2592.0000000000005" left="19.200000000000003" height="201.60000429153402" width="591.6000126600261" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="71">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="457.200012660026" height="144.000004291534" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="1" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol3</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="72">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue resultRef="73">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="1">
          <axisLine position="origin" positionticmark="0" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>4</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol3</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="74">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="75">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue resultRef="76">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

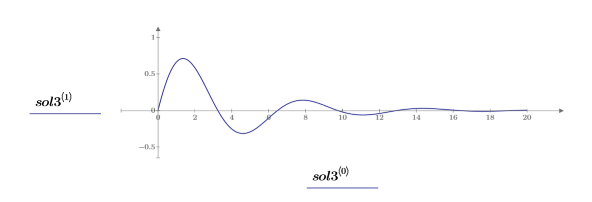
Soluzione feedback stato completo

1. Impostare le condizioni iniziali.

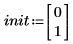
2. Scrivere l'equazione ODE in forma di matrice.

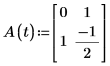
3. Definire le funzioni aggiuntive.

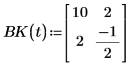
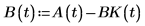
4. Chiamare la funzione statespace.

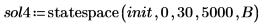
5. Tracciare un grafico della soluzione.

<region id="ID0EDR35" actualWidth="591.600012660026" actualHeight="201.60000429153402" top="3801.6000000000004" left="76.800000000000011" height="201.60000429153402" width="591.600012660026" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="82">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="457.200012660026" height="144.000004291534" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="1" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol4</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="83">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue resultRef="84">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="1">
          <axisLine position="origin" positionticmark="0" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>4</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol4</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="85">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="86">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue resultRef="87">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Argomenti correlati

Solutore ODE statespace

È stato utile?