Esempio: trasformazione inversa idft

Funzioni > Trasformate e filtri > Esempio: trasformazione inversa idft

Esempio: trasformazione inversa idft

Poiché la funzione idft è la trasformata inversa di dft, ci si aspetta che ripristini l'input dei dati originali nella trasformata complessa.

Utilizzo di vettori (1D)

1. Definire la lunghezza del vettore v.

2. Utilizzare la funzione exp per definire e valutare il vettore v.

Fare clic per copiare questa espressione

<region id="ID0EALVDB" actualWidth="265.80333333333328" actualHeight="100" top="307.20000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="210">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">v</id>
        <id labels="*" xml:space="preserve">m</id>
      </apply>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">exp</id>
          <apply>
            <mult />
            <apply>
              <mult />
              <imag symbol="j">1</imag>
              <apply>
                <div />
                <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">π</id>
                <real>3</real>
              </apply>
            </apply>
            <id xml:space="preserve">m</id>
          </apply>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

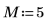
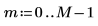
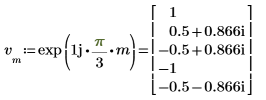
3. Utilizzare la funzione dft per calcolare la trasformata diretta del vettore v.

Fare clic per copiare questa espressione

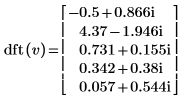
4. Utilizzare la funzione idft per calcolare la trasformata inversa del vettore v.

Fare clic per copiare questa espressione

5. Mostrare che la trasformata inversa della trasformata diretta del vettore v è il vettore originale v.

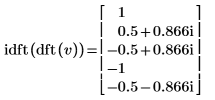Fare clic per copiare questa espressione

Fare clic per copiare questa espressione

I risultati sono identici.

Utilizzo di matrici (2D)

1. Definire e valutare la matrice C.

Fare clic per copiare questa espressione

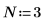
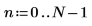
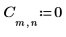
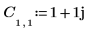
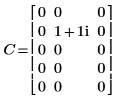
2. Utilizzare la funzione dft per calcolare la trasformata diretta della matrice C.

Fare clic per copiare questa espressione

3. Utilizzare la funzione idft per calcolare la trasformata inversa della matrice C.

Fare clic per copiare questa espressione

4. Mostrare che la trasformata inversa della trasformata diretta della matrice C è la matrice originale C.

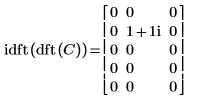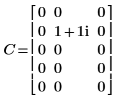Fare clic per copiare questa espressione

Fare clic per copiare questa espressione

I risultati sono identici.

Dimostrazione della somma sottostante alla base di idft

Studio unidimensionale

1. Utilizzare la funzione exp e l'operatore di somma per calcolare la trasformata inversa del vettore v.

<region id="ID0EE6VDB" actualWidth="155.60999999999999" actualHeight="50.000000000000007" top="1843.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="240">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">z</id>
        <id labels="*" xml:space="preserve">m</id>
      </apply>
      <apply>
        <summation />
        <lambda>
          <boundVars>
            <id xml:space="preserve">p</id>
          </boundVars>
          <parens>
            <apply>
              <mult />
              <apply>
                <indexer />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
                <id xml:space="preserve">p</id>
              </apply>
              <apply>
                <pow />
                <apply>
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ω</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
                </apply>
                <apply>
                  <mult />
                  <apply>
                    <neg />
                    <id xml:space="preserve">m</id>
                  </apply>
                  <id xml:space="preserve">p</id>
                </apply>
              </apply>
            </apply>
          </parens>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <apply>
            <minus />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
            <real>1</real>
          </apply>
        </upperBound>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

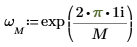
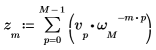
2. Confrontare la trasformata diretta risultante del vettore v con l'output della funzione dft.

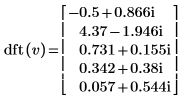Fare clic per copiare questa espressione

Fare clic per copiare questa espressione

I risultati sono identici.

3. Utilizzare l'operatore di somma per calcolare la trasformata inversa del vettore v.

<region id="ID0ECEWDB" actualWidth="173.77666666666664" actualHeight="50.75866666666667" top="2112.0000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="246">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">r</id>
        <id labels="*" xml:space="preserve">m</id>
      </apply>
      <apply>
        <scale />
        <apply>
          <div />
          <real>1</real>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
        </apply>
        <apply>
          <summation />
          <lambda>
            <boundVars>
              <id xml:space="preserve">p</id>
            </boundVars>
            <parens>
              <apply>
                <mult />
                <apply>
                  <indexer />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">v</id>
                  <id xml:space="preserve">p</id>
                </apply>
                <apply>
                  <pow />
                  <apply>
                    <indexer />
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ω</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
                  </apply>
                  <apply>
                    <mult />
                    <id xml:space="preserve">m</id>
                    <id xml:space="preserve">p</id>
                  </apply>
                </apply>
              </apply>
            </parens>
          </lambda>
          <lowerBound>
            <real>0</real>
          </lowerBound>
          <upperBound>
            <apply>
              <minus />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
              <real>1</real>
            </apply>
          </upperBound>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

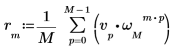
4. Confrontare la trasformata inversa risultante del vettore v con l'output della funzione idft.

Fare clic per copiare questa espressione

Fare clic per copiare questa espressione

I risultati sono identici.

Studio bidimensionale

1. Utilizzare la funzione exp e l'operatore di somma per calcolare la trasformata diretta della matrice C.

<region id="ID0EMJWDB" actualWidth="135.11" actualHeight="47.2" top="2419.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="252">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">ω</id>
        <id labels="*" xml:space="preserve">N</id>
      </apply>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">exp</id>
        <apply>
          <div />
          <apply>
            <mult />
            <apply>
              <mult />
              <real>2</real>
              <id labels="CONSTANT" xml:space="preserve">π</id>
            </apply>
            <imag symbol="i">1</imag>
          </apply>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0E1JWDB" actualWidth="269.42666666666673" actualHeight="50.000000000000007" top="2476.8" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="254">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">Z</id>
        <sequence>
          <id labels="*" xml:space="preserve">m</id>
          <id labels="*" xml:space="preserve">n</id>
        </sequence>
      </apply>
      <apply>
        <summation />
        <lambda>
          <boundVars>
            <id xml:space="preserve">p</id>
          </boundVars>
          <apply>
            <summation />
            <lambda>
              <boundVars>
                <id xml:space="preserve">q</id>
              </boundVars>
              <parens>
                <apply>
                  <mult />
                  <apply>
                    <mult />
                    <apply>
                      <indexer />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">C</id>
                      <sequence>
                        <id xml:space="preserve">p</id>
                        <id xml:space="preserve">q</id>
                      </sequence>
                    </apply>
                    <apply>
                      <pow />
                      <apply>
                        <indexer />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ω</id>
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
                      </apply>
                      <apply>
                        <mult />
                        <apply>
                          <neg />
                          <id xml:space="preserve">m</id>
                        </apply>
                        <id xml:space="preserve">p</id>
                      </apply>
                    </apply>
                  </apply>
                  <apply>
                    <pow />
                    <apply>
                      <indexer />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ω</id>
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
                    </apply>
                    <apply>
                      <mult />
                      <apply>
                        <neg />
                        <id xml:space="preserve">n</id>
                      </apply>
                      <id xml:space="preserve">p</id>
                    </apply>
                  </apply>
                </apply>
              </parens>
            </lambda>
            <lowerBound>
              <real>0</real>
            </lowerBound>
            <upperBound>
              <apply>
                <minus />
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
                <real>1</real>
              </apply>
            </upperBound>
          </apply>
        </lambda>
        <lowerBound>
          <real>0</real>
        </lowerBound>
        <upperBound>
          <apply>
            <minus />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
            <real>1</real>
          </apply>
        </upperBound>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

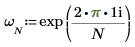
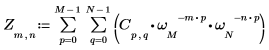
2. Confrontare la trasformata diretta risultante della matrice C con l'output della funzione dft.

Fare clic per copiare questa espressione

Fare clic per copiare questa espressione

I risultati sono identici.

3. Utilizzare l'operatore di somma per calcolare la trasformata inversa della matrice C.

<region id="ID0EYNWDB" actualWidth="303.16333333333336" actualHeight="50.75866666666667" top="2918.4000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="260">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="VARIABLE" xml:space="preserve">R</id>
        <sequence>
          <id labels="*" xml:space="preserve">m</id>
          <id labels="*" xml:space="preserve">n</id>
        </sequence>
      </apply>
      <apply>
        <scale />
        <apply>
          <div />
          <real>1</real>
          <apply>
            <mult />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
          </apply>
        </apply>
        <apply>
          <summation />
          <lambda>
            <boundVars>
              <id xml:space="preserve">p</id>
            </boundVars>
            <apply>
              <summation />
              <lambda>
                <boundVars>
                  <id xml:space="preserve">q</id>
                </boundVars>
                <parens>
                  <apply>
                    <mult />
                    <apply>
                      <mult />
                      <apply>
                        <indexer />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">C</id>
                        <sequence>
                          <id xml:space="preserve">p</id>
                          <id xml:space="preserve">q</id>
                        </sequence>
                      </apply>
                      <apply>
                        <pow />
                        <apply>
                          <indexer />
                          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ω</id>
                          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
                        </apply>
                        <apply>
                          <mult />
                          <id xml:space="preserve">m</id>
                          <id xml:space="preserve">p</id>
                        </apply>
                      </apply>
                    </apply>
                    <apply>
                      <pow />
                      <apply>
                        <indexer />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">ω</id>
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
                      </apply>
                      <apply>
                        <mult />
                        <id xml:space="preserve">n</id>
                        <id xml:space="preserve">p</id>
                      </apply>
                    </apply>
                  </apply>
                </parens>
              </lambda>
              <lowerBound>
                <real>0</real>
              </lowerBound>
              <upperBound>
                <apply>
                  <minus />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
                  <real>1</real>
                </apply>
              </upperBound>
            </apply>
          </lambda>
          <lowerBound>
            <real>0</real>
          </lowerBound>
          <upperBound>
            <apply>
              <minus />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M</id>
              <real>1</real>
            </apply>
          </upperBound>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

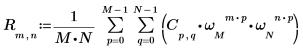
4. Confrontare la trasformata inversa risultante della matrice C con l'output della funzione idft.

Fare clic per copiare questa espressione

Fare clic per copiare questa espressione

I risultati sono identici.

Argomenti correlati

Trasformata discreta di Fourier di dati

È stato utile?