Esempio: trasformata diretta dft
Utilizzare la funzione dft per trovare la trasformata complessa di Fourier di un vettore o una matrice a valore reale o complesso di qualsiasi dimensione, con tempo o spazio costante tra i campioni.
Dati sinusoidali complessi 1D
Creare un insieme di dati complessi simulati con N punti dati alla spaziatura di campionamento T.
1. Definire il numero di punti dati.
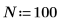
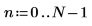
2. Definire il tempo T in cui vengono raccolti i campioni.
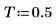
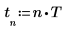
3. Impostare la frequenza angolare.
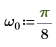
4. Utilizzare la funzione exp per definire una funzione esponenziale.
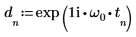
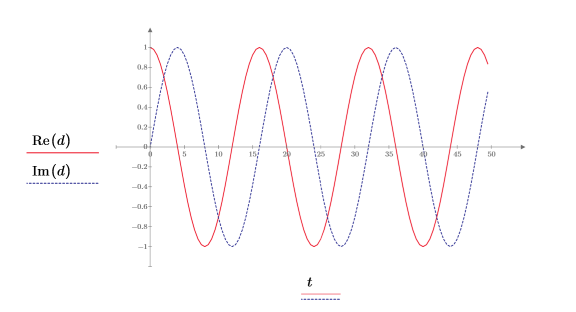
5. Utilizzare le funzioni Re e Im per estrarre e tracciare il grafico dei componenti reali e immaginari come funzioni di tempo.
6. Applicare la funzione dft per trasformare i dati nel dominio delle frequenze.
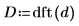
7. Raccogliere i valori assoluti di D in un nuovo array.
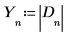
8. Definire la frequenza di campionamento e la frequenza corrispondente al n-esimo elemento nel vettore trasformato.
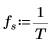
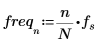
9. Utilizzare le funzioni match e max per trovare il picco e la frequenza corrispondente all'interno del segnale trasformato.
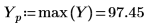
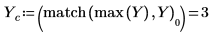
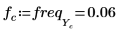
10. Tracciare il grafico del vettore trasformato e utilizzare indicatori verticali e orizzontali per contrassegnare la frequenza a cui l'ampiezza è al massimo.
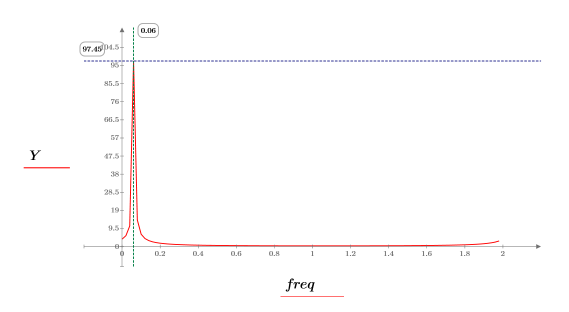
◦ La metà superiore dei campioni del dominio delle frequenze rappresenta le frequenze negative.
◦ Questo segnale complesso non ha contenuto a frequenze negative.
Ulteriori informazioni
• Di norma, per un vettore di dati reali v, il vettore dft(v) è complesso e simmetrico coniugato rispetto al valore centrale. Nel caso di una matrice, ogni colonna del risultato è simmetrica coniugata.
• Per qualsiasi input di array quadrato A, dft(A) è simmetrico.
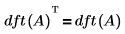
• In base al teorema di campionamento di Nyquist, la frequenza di campionamento deve essere almeno due volte la frequenza più alta che si desidera venga risolta tramite la trasformata di Fourier.
• L'algoritmo dei divisori dei numeri primi utilizzato nella trasformata rapida di Fourier rallenta quando il numero di punti dati è un numero primo grande. Benché questo problema potrebbe non verificarsi mai, tenere presente questa considerazione se è necessario utilizzare numeri primi di punti dati molto grandi.