Procedimiento para evaluar integrales de forma simbólica
1. Inserte un operador integral.
2. Escriba la expresión en el marcador a la derecha del signo de integral.
3. Escriba la variable de integración x en el marcador a la derecha del símbolo d.
4. Inserte el operador de evaluación simbólica.
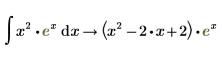
La integral indefinida solo se puede evaluar con el operador de evaluación simbólica. |
5. Para tomar la integral definida de la misma función, de 0 a 5, escriba 0 en el marcador inferior de la integral. Escriba 5 en el marcador superior y repita los pasos del 2 al 4.
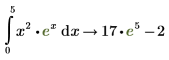
6. Para tomar la integral definida de la misma función cuando al menos uno de los límites es una variable no definida, repita los pasos del 2 al 4. A continuación, inserte los límites inferior y superior de la integral.
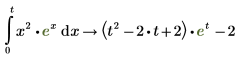
Al evaluar una integral definida en la que al menos uno de los límites esté sin definir, el motor simbólico supone que el límite superior es mayor que el límite inferior.
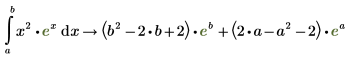
7. Para asignar los resultados de la evaluación simbólica a una función, defina una función de la siguiente forma:
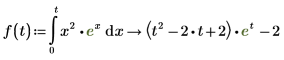
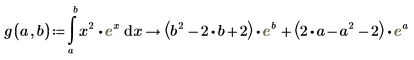
Valor principal de Cauchy
El valor principal de Cauchy de la integral sobre un punto c, en el intervalo (a,b) se define mediante la siguiente expresión:
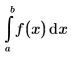
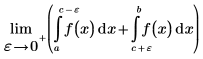
La finalidad del valor principal de Cauchy es definir el valor de la integral cuando la función f presenta un punto de singularidad en c. Por ejemplo, la siguiente integral presenta un punto de singularidad en c=0 y la evaluación simbólica devuelve un error.
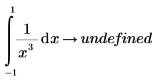
Para buscar el valor principal de Cauchy de la integral, añada el modificador cauchy.
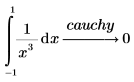
La evaluación simbólica de integrales que requieren el análisis de Cauchy devuelve un resultado de undefined, salvo que se especifique la palabra clave cauchy. |