Método de relajación para una ecuación diferencial parcial (PDE)
• relax(A, B, C, D, E, S, U, rjac)
• multigrid(M, ncycle)
Permite devolver una matriz cuadrada en la que la posición de un elemento en la matriz corresponde a su posición dentro de una región cuadrada, y el valor de un elemento se aproxima a la solución de la ecuación diferencial parcial (PDE) de Poisson
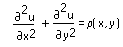
en ese punto. La función relax resuelve la ecuación de Poisson mediante el método de Gauss-Seidel modificado con sobrerrelajación sucesiva sobre la cuadrícula.
La función multigrid la resuelve en el caso especial de que todas las condiciones de límite en U sean cero, mediante el método multigrid.
• Si las condiciones de límite son constantes e iguales en los cuatro lados, transforme la ecuación para tener cero condiciones de límite en todos los lados y utilice multigrid, ya que es más rápido y fácil de configurar.
• La ecuación de Poisson reduce la ecuación de Laplace en el caso de que ρ = 0.
• Si intenta resolver una PDE hiperbólica o parabólica o un sistema de PDE, utilice numol.
Argumentos
• A, B, C, D, E son matrices cuadradas reales del mismo tamaño que contienen coeficientes de la aproximación de Laplace discretizada a la función u en los cuatro vecinos más cercanos y el punto de aproximación.
• S es una matriz cuadrada que contiene el término origen en cada punto dentro del cuadrado.
• U es una matriz cuadrada que contiene valores de límite a lo largo de los bordes de la región y la aproximación inicial para la solución dentro de la región.
• rjac es un valor real 0 < rjac < 1, el radio espectral de la iteración de Jacobi. Esto controla la convergencia del algoritmo de relajación.
El valor óptimo de rjac depende de los detalles del problema, pero r es un buen valor de partida, donde n es el número de puntos en cada dirección de la cuadrícula:
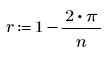
• M es una matriz cuadrada 1 + 2n cuyos elementos corresponden al término origen en el punto correspondiente en el dominio cuadrado.
• ncycle es el número entero de ciclos en cada nivel de la iteración multigrid.
Un valor ncycle de 2 generalmente ofrece una buena aproximación a la solución.