Regresión de función racional
• rationalfit(vx, vy, conf, m, n, [Stdy], [LBUB], [Acc], ["noscale"]): permite devolver parámetros y sus límites de confianza para un ajuste polinomial racional de orden m y n en la parte superior e inferior, o un chi-cuadrado residual permisible si la función debe permitir determinar el orden óptimo. Se consigue el nivel de confianza conf, con desviaciones estándar opcionales Stdy y límites opcionales inferiores y superiores para valores de parámetro aceptables. Si se facilita el argumento de cadena opcional "noscale", no se aplicará escala a los datos de entrada en el rango de 0 a 1 antes del cálculo.
• rationalfitnp(vx, vy, conf, m, n, [Stdy], [LBUB], [Acc], ["noscale"]): igual que rationalfit, pero evita los polos en la función racional resultante. El valor por defecto de Acc es 10-7.
La función de ajuste racional tiene la forma:
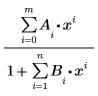
donde m y n son el grado deseado de numerador y denominador, respectivamente.
La salida de rationalfit, o de rationalfitnp, es una matriz de tres columnas en la que la primera columna contiene los valores de los parámetros ajustados, y la segunda y la tercera columnas contienen los límites izquierdo y derecho, respectivamente, para el intervalo de confianza de los parámetros.
Argumentos
• vx, vy son los vectores de valores de datos reales con la misma longitud.
• conf es el límite de confianza deseado, un porcentaje que se expresa con un número comprendido entre 0 y 1, ambos inclusive.
• m, n son números enteros de órdenes polinomiales para el numerador y el denominador de la función racional que se debe ajustar. La suma de m y n no puede superar la longitud de vx.
• Stdy (opcional) es un vector de desviaciones estándar en y. Stdy debe tener la misma longitud que vy.
• LBUB (opcional) es una matriz de dos columnas con límites inferiores y superiores para los parámetros, con filas m + n.
• Acc (opcional) es una precisión de convergencia. El valor por defecto de Acc es 10–7.
• "noscale" (opcional) es un argumento de cadena. Si se facilita este argumento, no se aplicará escala a los datos de entrada en el rango de 0 a 1 antes del cálculo.
Si utiliza más de uno de los argumentos opcionales, deberá especificarlos en su orden relativo, tal como se muestra en las definiciones de funciones.