Ejemplo: regresión de función racional 2
rationalfitnp - Sin polos
Utilice las funciones rationalfit y rationalfitnp para realizar la regresión de función racional. Si utiliza la función rationalfitnp en vez de la función rationalfit, la solución al problema tradicional de mínimos cuadrados se comprueba en busca de raíces del denominador dentro del intervalo de ajuste. Si no hay polos, se devuelve el ajuste generado. Si hay polos, se añaden restricciones adicionales al problema de optimización no lineal.
1. Defina un conjunto de datos modificando ligeramente la función inversa de x.
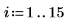
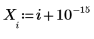
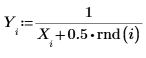
2. Especifique un orden para el numerador y el denominador de la función racional.
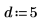
La función de ajuste tiene la siguiente forma:
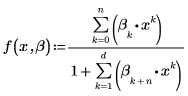
3. Defina un límite de confianza y un vector de desviaciones estándar.
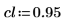
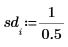
4. Llame a las funciones rationalfit y rationalfitnp.
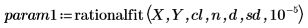 | 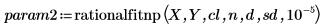 |
 |  |
Para param1 y param2, la primera columna contiene los parámetros y las demás columnas contienen los límites inferior y superior de cada parámetro en el límite de confianza definido anteriormente.
5. Trace el conjunto de datos y las dos curvas de regresión.
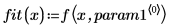
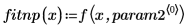
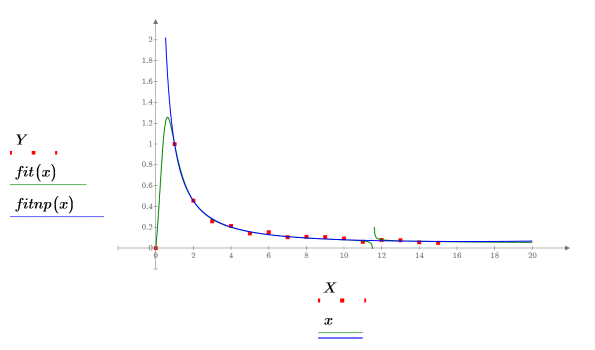
La función rationalfitnp ha quitado el polo. Su polinomio denominador se proyecta de la siguiente forma:
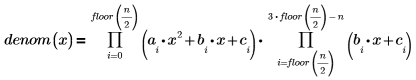
Para evitar el polo, se añadieron las siguientes restricciones:
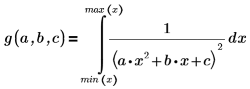
 |  |
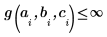 | 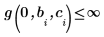 |
LeastSquaresFit
Compare las curvas de ajuste devueltas por rationalfitnp y LeastSquaresFit. La función LeastSquaresFit realiza el mismo algoritmo que la función rationalfitnp, pero requiere valores de prueba y límites de confianza para los parámetros. Es recomendable hacer esto cuando desee que el término constante se encuentre en el numerador, en vez de en el denominador.
1. Defina la función de ajuste.
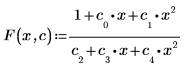
2. Defina valores de prueba para los parámetros.
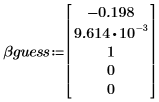
3. Defina las condiciones de límite inferior y superior para los parámetros.

4. Llame a la función LeastSquaresFit.
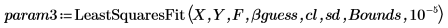
5. Trace el conjunto de datos y las curvas de ajuste devueltos por las funciones rationalfitnp y LeastSquaresFit.
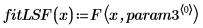
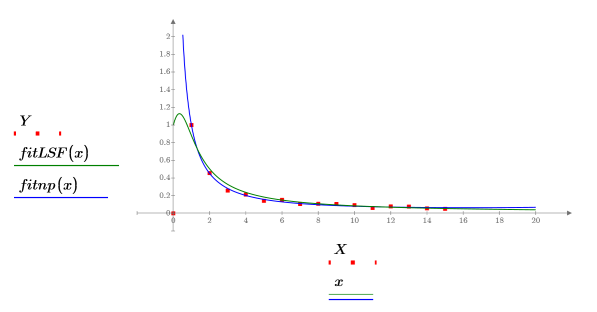
Los métodos de filtrado o transformación de datos que sesguen los datos hacia una línea recta antes de realizar un ajuste de función racional aumentarán considerablemente la velocidad de convergencia de la función rational y pueden tener la ventaja colateral de eliminar los polos no deseados. |