Curtosis y sesgo
• kurt(A, B, C, ...): permite devolver la curtosis de los elementos A, B, C, .... La curtosis se define del siguiente modo:
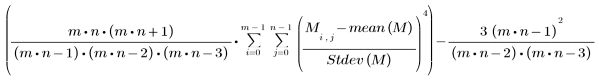
La curtosis de un conjunto de valores indica si la distribución es plana o con picos en comparación con la distribución normal:
Value | Forma de distribución |
|---|---|
kurt = 0 | Distribución normal |
kurt > 0 | Distribución con picos relativos |
kurt < 0 | Distribución relativamente plana |
• skew(A, B, C, ...): permite devolver el sesgo de los elementos A, B, C, .... El sesgo se define del siguiente modo:
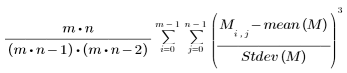
El sesgo de un conjunto de valores mide la asimetría en torno a la media:
Value | Forma de distribución |
|---|---|
skew = 0 | La distribución es simétrica en torno a la media, como en la distribución normal. |
skew > 0 | La "cola" de la distribución se extiende hacia los valores positivos. |
skew < 0 | La "cola" de la distribución se extiende hacia los valores negativos. |
Argumentos
• A, B, C, ... son escalares o arrays. Debe haber al menos cuatro elementos en los argumentos para kurt y al menos tres para skew.
• M es un array creado con los argumentos de la función A, B, C, .... La desviación estándar de M debe ser distinta de cero.