Ejemplo: uso de unidades con funciones de interpolación polinomial
1. Defina dos vectores de entrada y una variable independiente.
 |
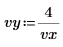 |
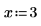 |
2. Defina las unidades.
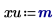
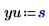
3. Evalúe los vectores de entrada y la variable de entrada.
 |  | 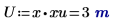 |
La unidad de la variable independiente U debe coincidir con la unidad del vector del primer argumento. |
Interpolación polinomial
1. Utilice la función polyint para evaluar la función de interpolación en los valores de las variables independientes especificadas.
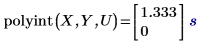
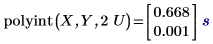
La búsqueda de U en el vector de entrada X tiene como resultado una coincidencia y el valor exacto correspondiente del vector Y es 1.333 con un error de cero. No obstante, 2U no tiene ninguna coincidencia exacta en X, lo que produce un valor interpolado con un error distinto de cero.
2. Utilice la función length para determinar la longitud de los vectores de entrada y, a continuación, cree un programa corto para evaluar las funciones de interpolación en diferentes puntos. Visualice los puntos interpolados en la primera columna y los valores de error en la segunda.
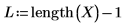

La variable u debe ser un escalar y la unidad mse añade como parte del argumento de la función.
3. Guarde los puntos de interpolación y los valores de error en dos vectores diferentes.
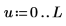
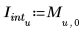
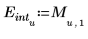
4. Trace los puntos de interpolación junto con el envolvente del error.
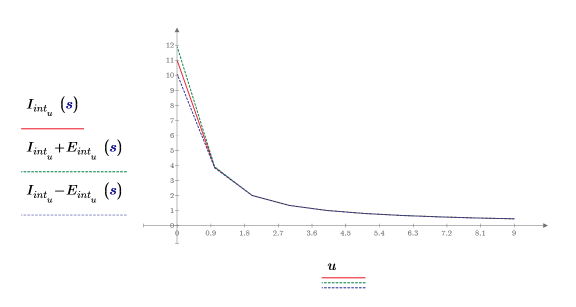
El error comienza siendo relativamente grande y se convierte en negligente después del segundo punto de interpolación.
Iteración polinomial
1. Utilice la función polyiter para evaluar la función de iteración en el valor de la variable independiente especificada, el número de iteraciones máximas y la tolerancia.
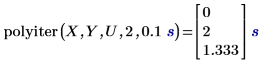
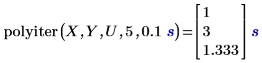
• El algoritmo se detiene si los dos últimos cálculos aproximados iterados del punto de datos coinciden con el valor de tolerancia, o si el número de iteraciones alcanza el número máximo de iteraciones permitido. • El primer resultado muestra que la convergencia de la función de iteración ha fallado después de alcanzar el número máximo permitido de dos iteraciones, por lo que ha devuelto el elemento correspondiente en el vector Y. • El segundo resultado muestra que la función de iteración ha convergido después de la tercera iteración y que no ha alcanzado el número máximo permitido de cinco iteraciones. |
2. Utilice un programa corto para evaluar la función de iteración en diez puntos diferentes. Utilice el argumento de la función para añadir el valor del error a la cuarta columna de la matriz devuelta, que muestra el estado de combinación en la primera columna, el número de iteraciones utilizadas en la segunda columna y los valores iterados en la tercera columna.

3. Guarde los puntos de interpolación y los valores de error en vectores diferentes.
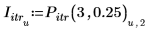
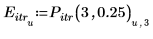
4. Trace los puntos de iteración de 3 iteraciones y un error de 0.25.
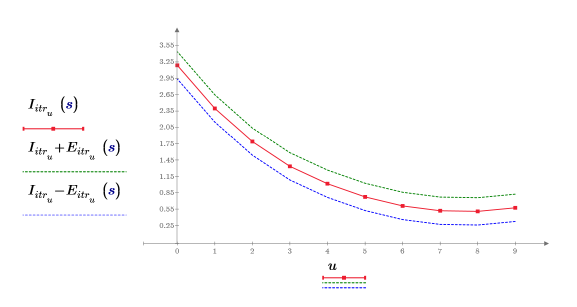
El error es constante en todos los puntos de interpolación.
5. Compare los resultados devueltos de la interpolación y la iteración con el número máximo de iteraciones definido en 3 y el error definido en 0.25.
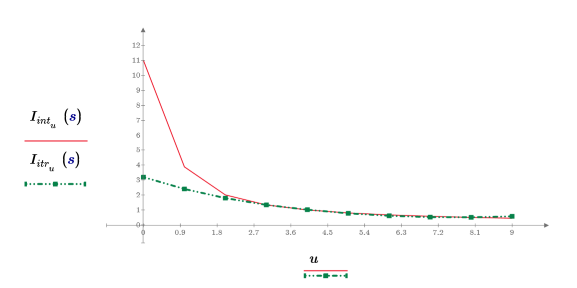
6. Muestre que el resultado de la interpolación es idéntico al resultado de la iteración cuando el número de iteraciones está definido en un número alto y el error está definido en cero.
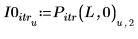
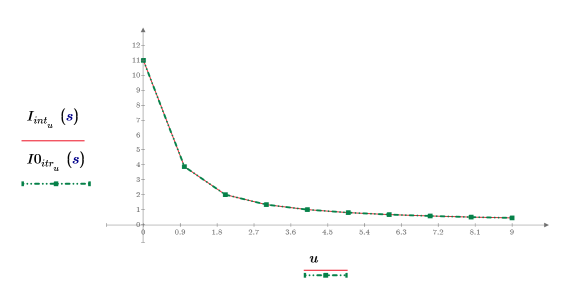
El número máximo de iteraciones debe ser inferior a la longitud de los vectores de entrada.