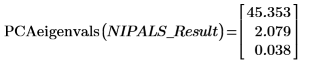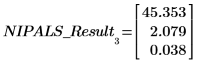Ejemplo: análisis de componentes principales 1
Use las funciones Nipals, loadings, scores, PCAeigenvals y PCAvariance para realizar un análisis de componentes principales (PCA).
La función de Nipals
1. Defina un conjunto de datos donde cada columna corresponda a una variable.


2. Trace el conjunto de datos.
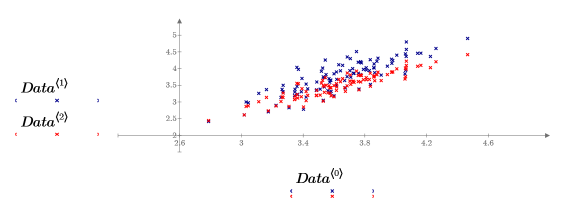
En este gráfico, el plano X-Y y el plano X-Z se superponen para mostrar la tendencia de los datos. De hecho, los datos constituyen una nube elíptica de puntos que casi recae sobre un plano. Las tres variables están relacionadas linealmente y la desviación con respecto a un plano perfecto se debe al ruido.
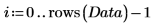
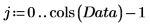
4. Utilice la función mean para buscar la media de los datos y, a continuación, réstela de cada una de las variables para centrar los datos.
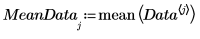
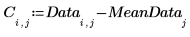
5. Trace los datos centrados.
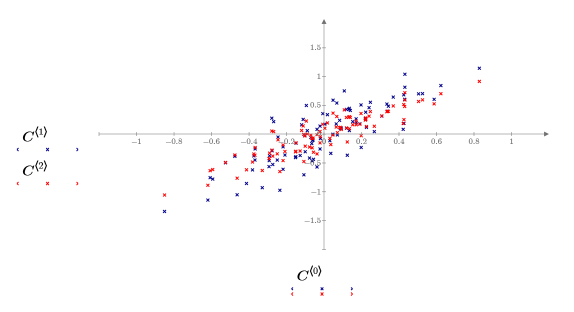
• Ahora los datos están centrados alrededor del origen. Este es uno de los pasos que la función Nipals realiza automáticamente. • En muchas aplicaciones de PCA, también es recomendable aplicar una escala a los datos de modo que las variables tengan pesos iguales como, por ejemplo, cuando variables diferentes tienen unidades diferentes. El escalado de todas las variables (cada columna de datos) a una varianza unitaria es habitual, pero no es adecuado para estos datos, por lo que no se debe aplicar ningún escalado. |
6. Utilice la función Nipals para crear un nuevo espacio de variable. Utilice tres componentes principales (el máximo posible, ya que solo había tres variables para empezar).
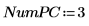
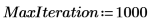
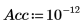
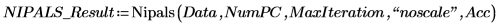
La salida de la función Nipals es una matriz anidada de 6 matrices individuales. Úsela para buscar las funciones loadings, scores, eigenvals y eigenvecs de los datos. Si es necesario, use la función Nipals2 y las últimas dos matrices para extraer componentes adicionales.
Cargas y puntuaciones
1. Llame a la función loadings para recuperar los datos de la segunda matriz de NIPALS_Result.
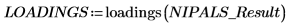
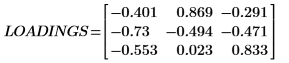
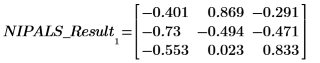
Cada columna de LOADINGS es un vector de carga.
2. Llame a la función scores para recuperar los datos de la primera matriz de NIPALS_Result.
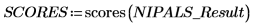

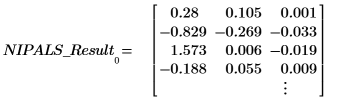
Las puntuaciones representan las proporciones en que los vectores de carga se añaden para recrear los espectros originales. Considérelas identidades. Datos = LOADINGS x SCOREST.
3. Trace los datos almacenados en la matriz SCORES.
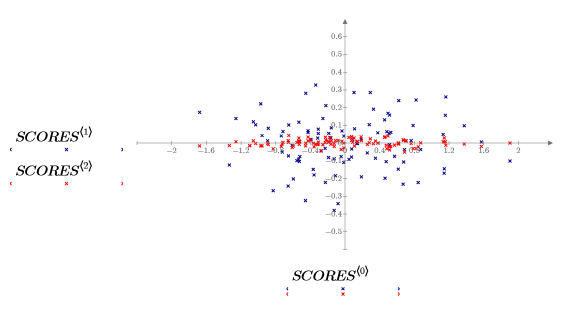
Los datos se han girado para que la primera variable pueda explicar la máxima cantidad de varianza. En el gráfico, esto se representa mediante el eje longitudinal de la nube elíptica, que ahora es paralelo al eje X. Los valores de la tercera variable, paralela al eje Z, son muy pequeños. Esta variable se puede descartar en la mayoría de los casos. Ha comprimido los datos.
Autovalores y varianza del análisis PCA
1. Use la función PCAvariance para devolver las varianzas acumuladas de los tres componentes principales.
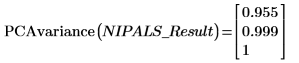
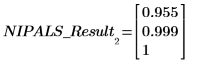
Los dos primeros componentes constituyen el 99.9 % de la varianza del sistema.
2. Use la función PCAeigenvals para extraer los autovalores de los componentes principales.