Ejemplo: generadores de ruido
Utilice las funciones whiten, gaussn y onefn para simular ruidos blancos, gaussianos y 1/f, respectivamente.
Ruido blanco
La función whiten simula el ruido producido por orígenes independientes N, cada uno con una salida aleatoria tras una distribución uniforme comprendida entre -0.5 y 0.5.
1. Utilice la función whiten para evaluar la función de ruido blanco para seis orígenes de ruido independientes.

La evaluación repetida de la función whiten genera un conjunto diferente de elementos de vector.
2. Considere un vector de salida un poco mayor.
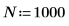
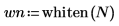
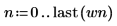
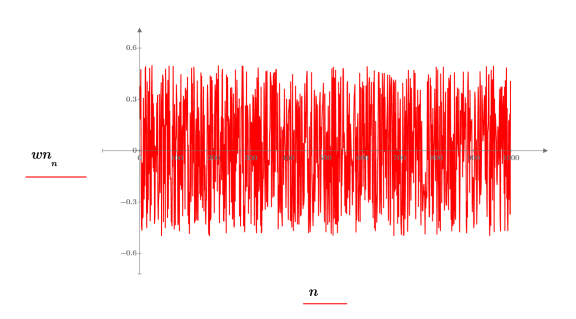
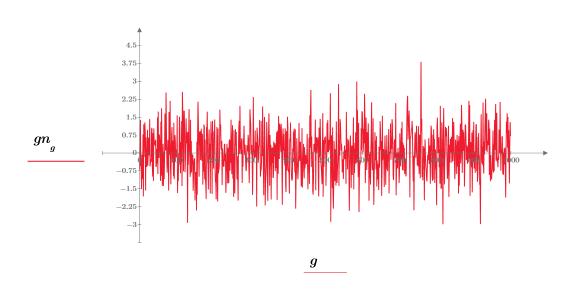
3. Trace la función de ruido blanco.
4. Utilice las funciones mean y stdev para calcular la desviación media y estándar del vector de ruido blanco.
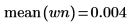
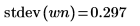
5. Muestre el valor teórico de la media y, a continuación, utilice la función var para calcular la desviación estándar.
En el gráfico se muestra que la señal wn tiene una media teórica de 0. | |
La desviación estándar es la raíz cuadrada de la varianza. | 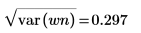 |
6. Compare los valores calculados de la desviación media y estándar con los valores teóricos y verifique que no haya una desviación significativa entre ambos.
Ruido gaussiano
La función gaussn simula un número x de orígenes de ruido independientes, cada uno tras una distribución de probabilidad gaussiana con una media de 0 y una desviación estándar de 1.
1. Evalúe la función de ruido gaussian para seis orígenes de ruido independientes.

Teóricamente, los elementos de un vector pueden tener cualquier valor real, pero lo más probable es que su valor se encuentre entre -3 y +3. Esto se puede verificar pulsando F5 para volver a calcular la función.
2. Trace una secuencia gaussiana de muestra.
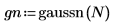
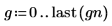
3. Prepare los datos gaussianos para un gráfico de histograma en forma de campana agrupando los valores en 20 contenedores de 0.05 de ancho.
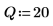
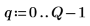
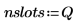
4. Defina el vector que sujeta los bordes de los contenedores y, a continuación, defina el contorno del extremo derecho.
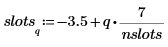
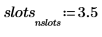
5. Utilice la función hist para crear el histograma y, a continuación, trácelo como un gráfico de barras.
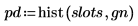
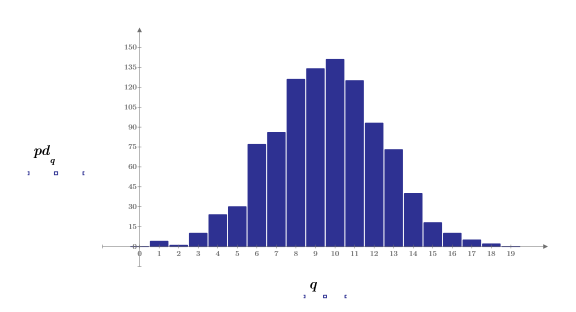
6. Compare la desviación media y estándar de la muestra con los valores esperados de 0 y 1.
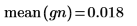
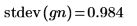
Ruido 1/f
La función onefn calcula una aproximación de ruido 1/f mediante una rutina basada en un algoritmo desarrollado por Richard Voss (consulte la columna de Martin Gardner en Scientific American, abril de 1978).
1. Utilice la función onefn para generar un vector 1/f de 1000 puntos.
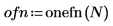
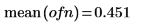
2. Ajústela a la media 0.
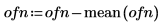
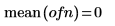
3. Trace los datos del vector.
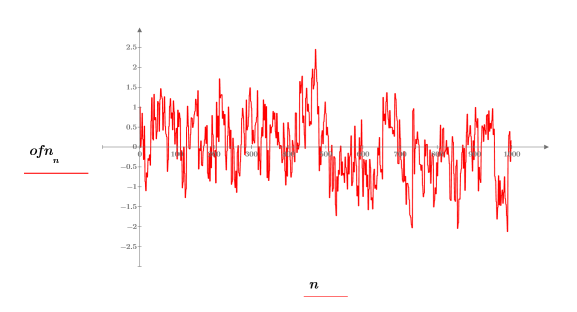
El ruido 1/f se encuentra en las señales de muchos fenómenos naturales y creados por el hombre, incluida la música, las señales cerebrales, el tiempo, los movimientos de la bolsa de acciones y otros sistemas de interacción jerárquica. Si, por ejemplo, se fuera a digitalizar muestras musicales de una variedad de estilos (rock, jazz, clásica), se vería que sus espectros de potencia se encuentran muy cerca en la distribución del ruido 1/f.
4. Utilice la función lcorr para comparar la estructura estadística de este ruido con el ruido blanco generado anteriormente mediante el cálculo de sus autocorrelaciones.
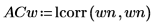
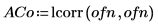
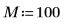
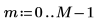
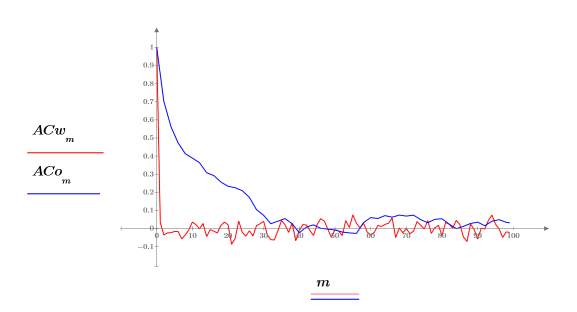
A diferencia del ruido blanco, el ruido generado por onefn presenta una correlación en decrecimiento a medida que aumenta el retardo.
Comparación de señales de ruido con espectros de potencia
Las diferencias entre el ruido blanco y el ruido 1/f también se pueden apreciar comparando sus espectros de potencia.
1. Suponga que tiene 50 contenedores de grupos de frecuencia de 20.
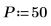
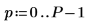
2. Utilice las funciones mag y dft para calcular la magnitud cuadrática de los espectros de frecuencia para cada señal.
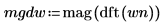
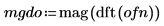
3. Suavice el resultado calculando la media de los grupos de frecuencia.
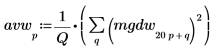
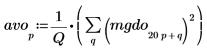
4. Trace el espectro de ruido blanco.
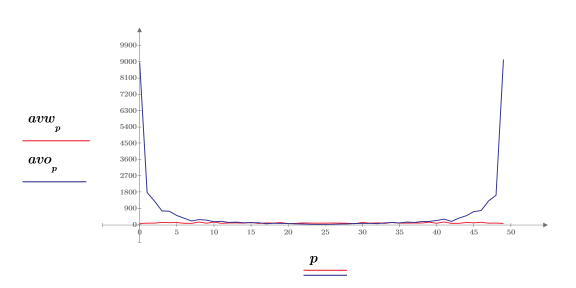
Tal y como se esperaba, el espectro de ruido blanco es básicamente plano. El espectro de magnitud de la aproximación de 1/f disminuye rápidamente cuando aumenta la frecuencia.
5. Utilice la función log para calcular el registro más informativo de la magnitud.
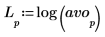
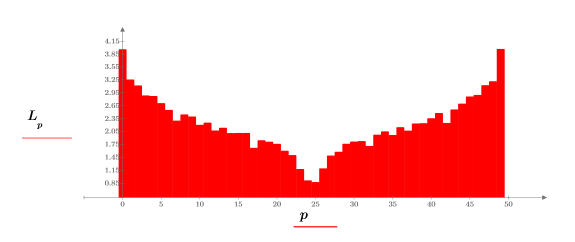
Experimento
Como experimento, intente crear un espectro de potencia de 1/f con fases aleatorias y tome la transformada inversa para obtener el vector de ruido.
1. Defina el ancho del espectro.
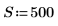
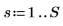
2. Utilice la función exp para crear la primera mitad de la transformada. Un espectro de potencia de 1/f se corresponde con un espectro de magnitud de 1/sqrt(f).
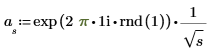
3. Calcule la segunda mitad de la transformada (para una señal real, la segunda mitad es conjugado simétrico alrededor del punto medio).
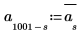
4. Defina la media del ruido en cero.
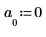
5. Utilice la función idft para obtener la transformada inversa de Fourier (transformada al dominio del tiempo).
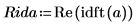
6. Trace los valores reales de la transformada inversa.
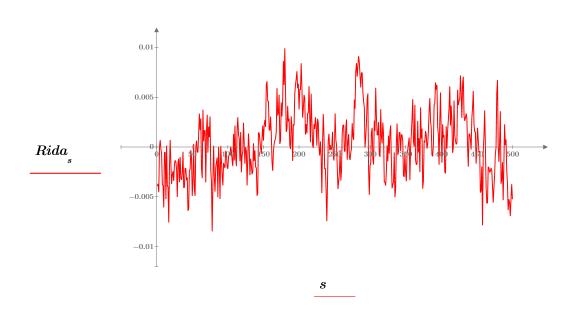
7. Utilice la función lcorr para calcular la curva de autocorrelación.
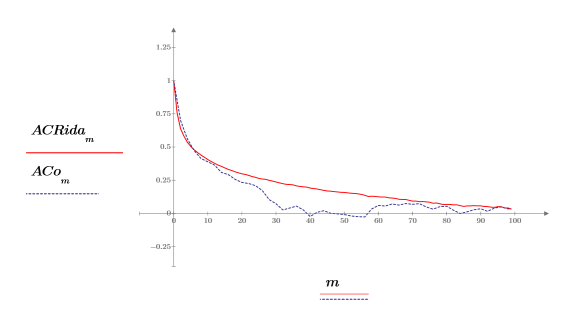
El comportamiento de la autocorrelación es similar a la salida de onefn, con una correlación de 1.0 en 0 y distintos grados de correlación en otros puntos.