Ejemplo: anulación de tendencias lineales
Utilice la función detrend para aproximarse a una tendencia lineal y quitarla de los datos usando una línea de trayectoria de ajuste de mínimos cuadrados.
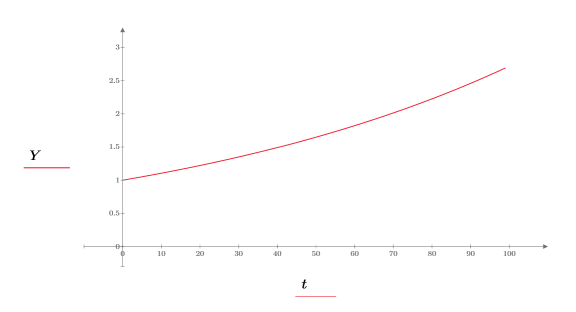
1. Defina una señal exponencial.
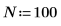
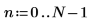
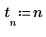
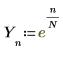
2. Trace la señal exponencial.
3. Utilice la función whiten para añadir ruido blanco a la señal.
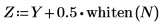
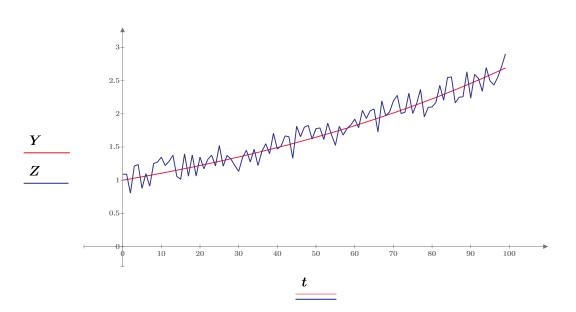
4. Trace la señal original y la señal ruidosa.
5. Aplique la función detrend a la señal contaminada por ruido.
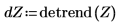
6. Trace la función original y las de anulación de tendencia.
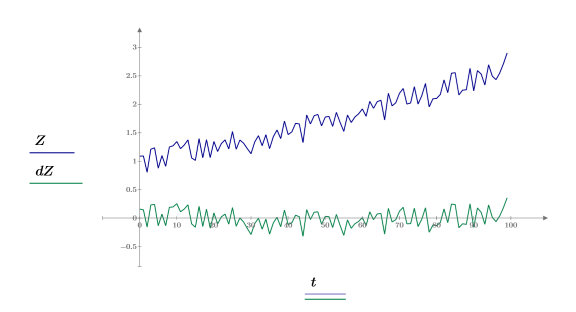
La desaparición de la tendencia lineal se puede demostrar además estudiando la línea de los mínimos cuadrados antes y después de quitar la tendencia.
7. Utilice las funciones slope e intercept para calcular la pendiente y la intercepción antes y después de la eliminación de la tendencia.
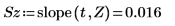 | 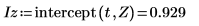 |
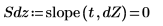 | 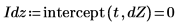 |
Esto ocurre siempre. La salida de detrend es un vector cuya línea de mínimos cuadrados es la línea horizontal que atraviesa el origen, es decir, la inclinación y la intercepción están muy próximas a 0.
Un efecto de detrend es que la media se ha quitado de los datos de entrada, como se puede observar consultando el término DC antes y después de quitar la tendencia.
8. Utilice la función dft para calcular el término DC (primero) antes y después de la eliminación de la tendencia.
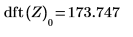
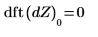
La función detrend realiza una sencilla tarea de preprocesamiento que a menudo antecede a una operación de suavizado. Tal y como se ha mencionado anteriormente, la anulación de tendencias también resulta útil a menudo como primer paso en la estimación del espectro.