Ejemplo: Spline de mínimo cuadrado
Spline2, Binterp y DWS
Utilice la función Spline2 para buscar el conjunto óptimo de nudos que Binterp necesita para calcular una interpolación spline de mínimos cuadrados.
1. Defina un conjunto de datos.

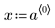 | 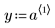 | 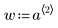 |
w es un vector de pesos que proporciona las desviaciones estándar aproximadas del error aleatorio en y.
2. Defina el grado de los polinomios spline deseados.
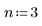
3. Llame a la función Spline2.
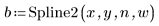

El primer elemento del vector b es el orden de B-spline. El segundo elemento proporciona el número de intervalos (knots - 1). Los elementos siguientes son los valores de nudo. Los demás elementos contienen los coeficientes de las funciones B-spline básicas.
El primer y el último nudo, cuando se generan automáticamente, coinciden con los puntos finales de los datos x originales.
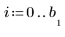
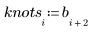
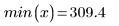 | 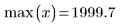 |
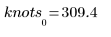 | 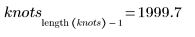 |
4. Llame a la función Binterp para un rango de valores que coincida con el rango de x.
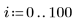
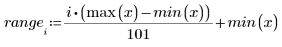

La fila i de spline1 contiene el valor interpolado, y la primera, segunda y tercera derivadas en el punto definido por el rango i.
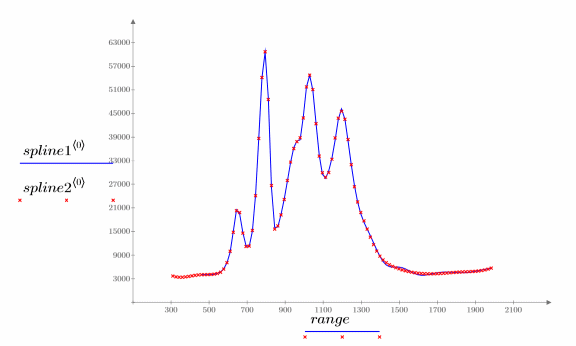
5. Trace los datos originales y el spline interpolado.
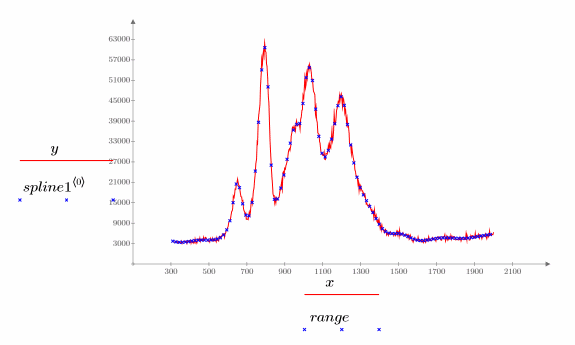
El número óptimo de nudos y su espaciado están determinados por la estadística de Durbin-Watson. Esta estadística debe tener un valor aproximado de 2 para que el ajuste sea adecuado. La estadística se puede buscar con la función DWS o mediante la extracción del elemento pertinente de la matriz b:
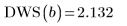
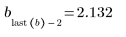
6. Utilice el último argumento opcional de Spline2, un porcentaje entre 0 y 1, para proporcionar un nivel de significancia o de rechazo para la prueba de Durbin-Watson.
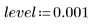
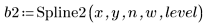
En general, aunque no siempre, los niveles de rechazo elevados producen más nudos y cálculos más largos.
7. Calcule el número de nudos que utiliza Spline2.
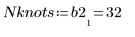
8. Llame a la función DWS para calcular la estadística de Durbin-Watson.
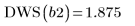
9. Trace los dos splines interpolados.
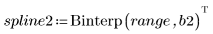
La interporlación se puede realizar sin pesos:
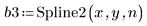
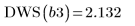
La interpolación se puede realizar sin pesos, pero es necesario un nivel de rechazo:
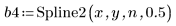
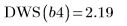
Derivadas del spline
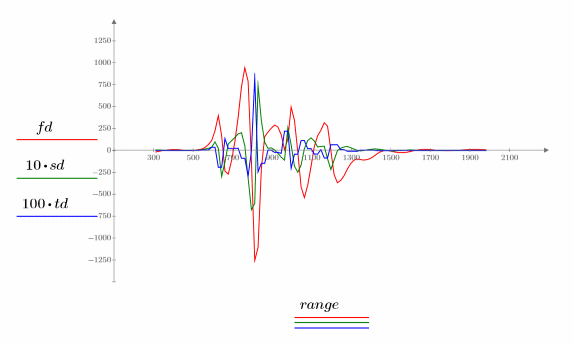
Trace las tres primeras derivadas del spline de interpolación.
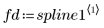
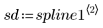
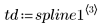
Suministro de nudos propios
Es posible proporcionar nudos propios para la interpolación B-spline.
1. Defina una cadena de nudos.
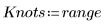
2. Trace el spline interpolado.
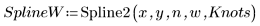
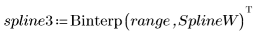
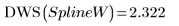
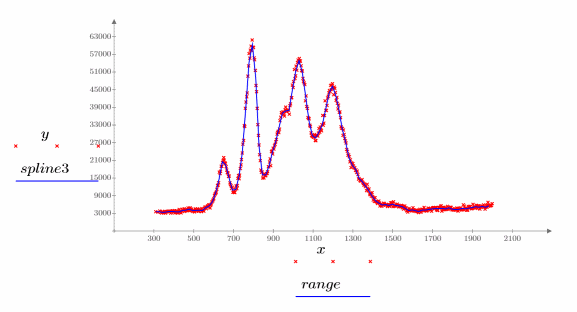
Se pueden proporcionar nudos sin vector de ponderación:

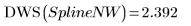
Valores atípicos
Se puede ver el efecto de quitar un valor atípico en la interpolación spline.
1. Llame a la función GrubbsClassic para detectar el punto que tiene más probabilidades de ser un valor atípico.

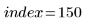
En la parte superior del segundo pico de datos, hay un punto sospechoso.
2. Quite el punto del conjunto de datos y la función de ponderación.
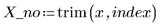
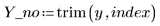
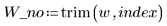
3. Llame a la función Spline2 para el nuevo conjunto de datos.
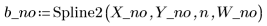
Según la estadística de Durbin-Watson, el ajuste ha mejorado:
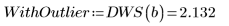
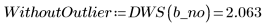
4. Compare los resultados de las interpolaciones en el valor de datos sospechoso:
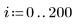
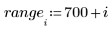
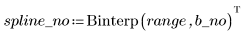
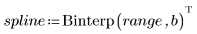
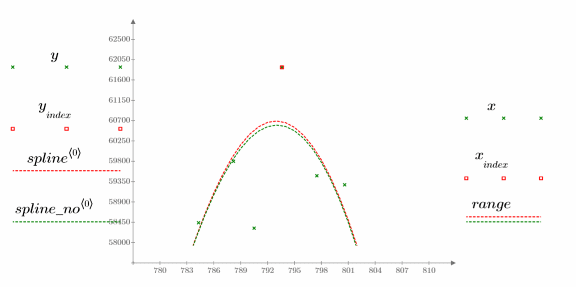
El spline desciende ligeramente cuando se quita el valor atípico.