Ejemplo: idft de transformación inversa
La función idft es la transformada inversa de dft y, por lo tanto, se espera que restaure la entrada de datos original a la transformada compleja.
Trabajo con vectores (1D)
1. Defina la longitud del vector v.
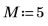
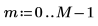
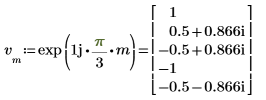
3. Utilice la función dft para calcular la transformada directa del vector v.
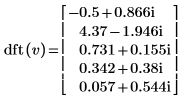
4. Utilice la función idft para calcular la transformada inversa del vector v.

5. Muestre que la transformada inversa de la transformada directa del vector v es el vector original v.
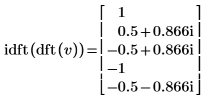 |  |
Los resultados son idénticos.
Trabajo con matrices (2D)
1. Defina y evalúe la matriz C.
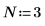
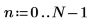
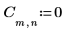
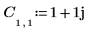
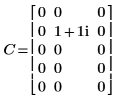
2. Utilice la función dft para calcular la transformada directa de la matriz C.

3. Utilice la función idft para calcular la transformada inversa de la matriz C.

4. Muestre que la transformada inversa de la transformada directa de la matriz C es la matriz original C.
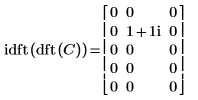 | 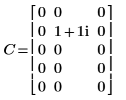 |
Los resultados son idénticos.
Demostración de la suma subyacente tras idft
Caso unidimensional:
1. Utilice la función exp y el operador de suma para calcular la transformada inversa del vector v.
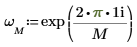
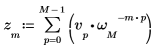
2. Compare la transformada directa resultante del vector v con la salida de la función dft.
 | 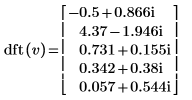 |
Los resultados son idénticos.
3. Utilice el operador de suma para calcular la transformada inversa del vector v.
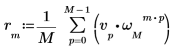
4. Compare la transformada inversa resultante del vector v con la salida de la función idft.
 |  |
Los resultados son idénticos.
Caso bidimensional:
1. Utilice la función exp y el operador de suma para calcular la transformada directa de la matriz C.
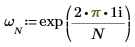
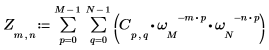
2. Compare la transformada directa resultante de la matriz C con la salida de la función dft.


Los resultados son idénticos.
3. Utilice el operador de suma para calcular la transformada inversa de la matriz C.
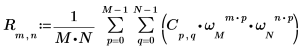
4. Compare la transformada inversa resultante de la matriz C con la salida de la función idft.


Los resultados son idénticos.