Ejemplo: introducción a las FFT
Las transformadas rápidas de Fourier (FFT) son un método numérico para expresar el contenido de frecuencia de un conjunto de datos medido a lo largo del tiempo. A menudo, los datos son continuos y constituyen una forma de onda. Para trabajar con los datos numéricamente, se muestrean a intervalos de tiempo regulares con determinada frecuencia de muestreo. En los diagramas siguientes se indican algunas formas de onda muestreadas y las magnitudes de sus transformadas de Fourier trazadas con respecto a la frecuencia.
Forma de onda de seno muestreada
1. Use la función sin para definir una forma de onda sinusoidal.
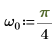
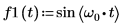
2. Defina el número de puntos de datos.
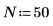
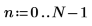
3. Defina la distancia entre muestras.
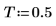
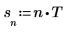
4. Defina la frecuencia de muestreo.
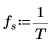
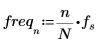
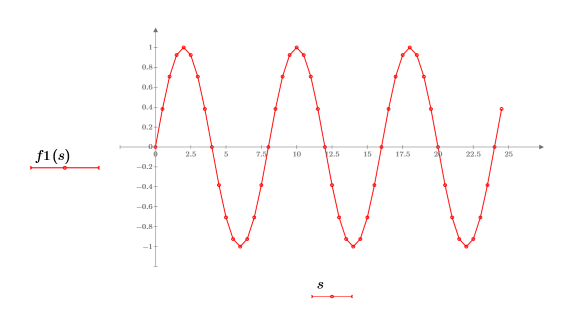
5. Trace la función sinusoidal.
6. Use la función dft para calcular la transformada de Fourier discreta.
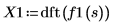
X1 es un vector de números complejos y reales.
7. Busque las frecuencias en las que se producen las magnitudes pico.
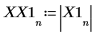
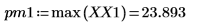
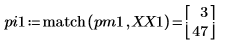
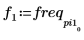
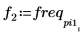
8. Trace la señal transformada y utilice los marcadores para mostrar la frecuencia y la magnitud de los picos.
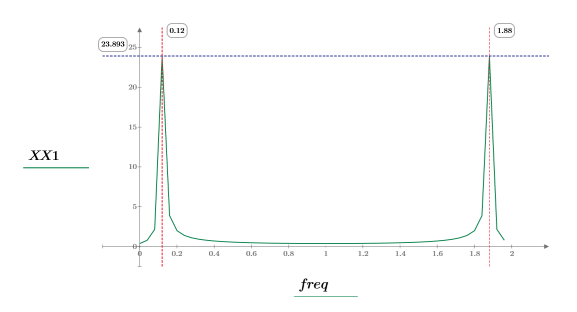
Forma de onda de coseno muestreada
1. Use la función cos para definir una forma de onda de coseno.
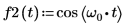
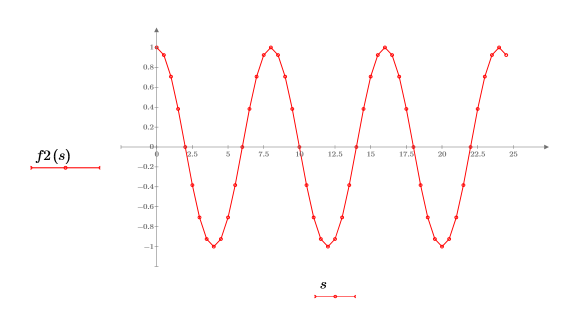
2. Trace la función de coseno.
3. Utilice la función dft para calcular las transformadas de Fourier discretas.
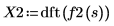
X2 es un vector de números complejos y reales.
4. Busque las frecuencias en las que se producen las magnitudes máximas.
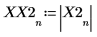
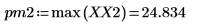
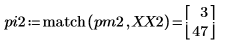
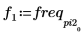
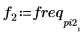
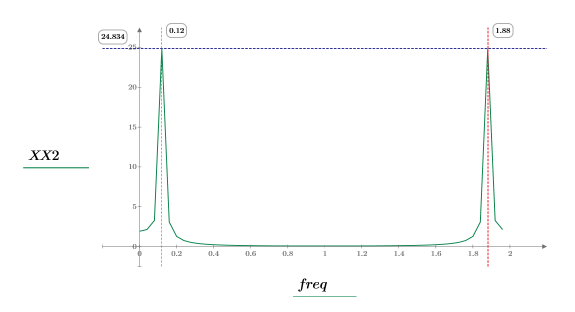
5. Trace la señal transformada y utilice los marcadores para mostrar la frecuencia y la magnitud de los picos.
Forma de onda exponencial muestreada
1. Use la función exp para definir una forma de onda exponencial.
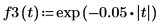
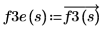
El operador de vectorización se utiliza para obtener los valores por elementos de la función porque el operador determinante dentro de la definición devuelve un solo valor escalar.
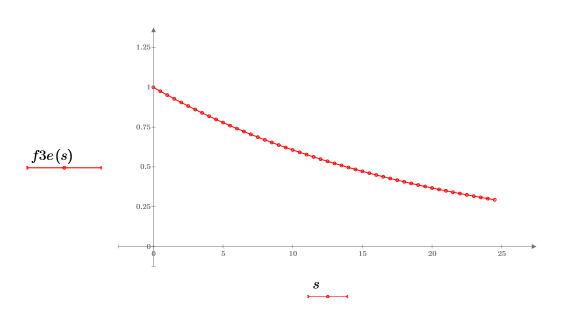
2. Trace la función exponencial.
3. Utilice la función dft para calcular la transformada de Fourier discreta.
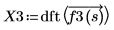
X3 es un vector de números complejos y reales.
4. Busque las frecuencias en las que se producen las magnitudes máximas.
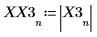
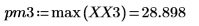
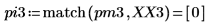
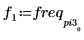
5. Trace la señal transformada y utilice los marcadores para mostrar la frecuencia y la magnitud de los picos.
Forma de onda de paso muestreada:
1. Use la función if para definir una forma de onda de paso.
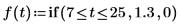
2. Calcule la magnitud de impulsión en cada intervalo.
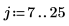
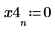
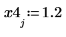
3. Trace la función escalón.
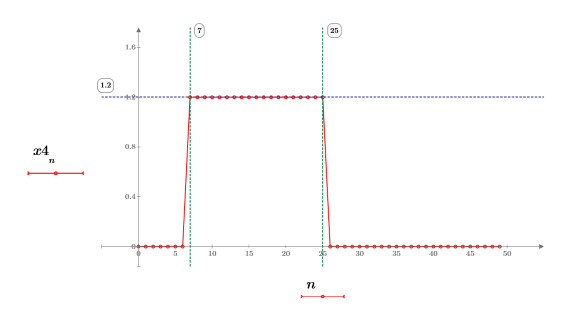
La magnitud es uniforme e igual a 1.2 entre 7 y 25.
4. Utilice la función dft para calcular la transformada de Fourier discreta.
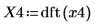
X4 es un vector de números complejos y reales.
5. Busque las frecuencias en las que se producen las magnitudes máximas.
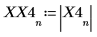
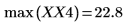
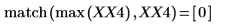
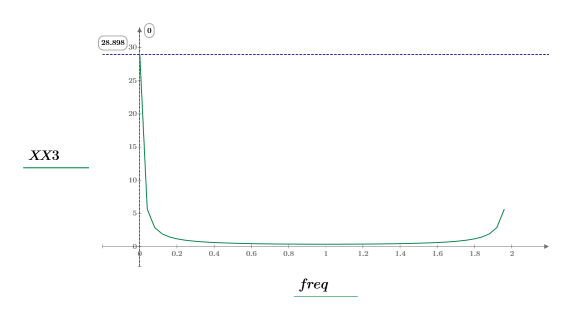
6. Trace la señal transformada y utilice los marcadores para mostrar la frecuencia y la magnitud de los picos.
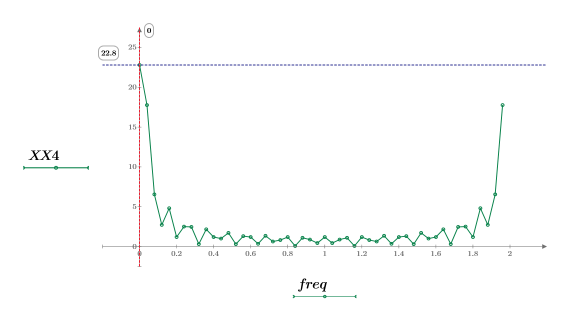
La magnitud máxima se da en freq0.