Ejemplo: pares de transformadas de Fourier
Defina el período, la frecuencia de muestreo y el número de muestras de una señal.
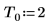 |
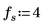 |
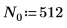 |
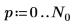 |
Señal sinusoidal
1. Utilice la evaluación simbólica para buscar la transformada de Fourier de una señal sinusoidal.
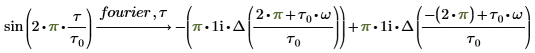
Al reorganizar los términos del resultado, se obtiene lo siguiente:
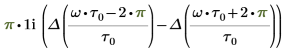
En el resultado se muestran dos componentes que utilizan la función delta de Dirac (impulso unidad) Δ.
2. Utilice la función sin para definir una señal sinusoidal.
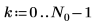
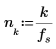
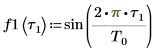
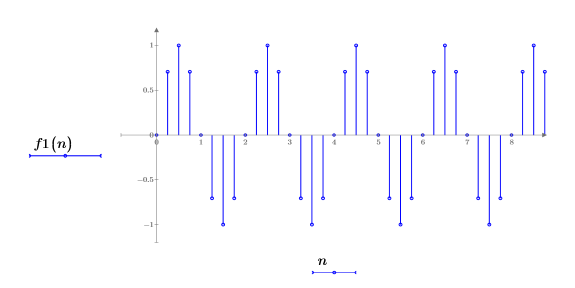
3. Trace los primeros elementos de la función f1.
4. Utilice la función dft para buscar la transformada de Fourier discreta de la señal.
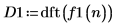
5. Trace los dos componentes de la transformada de Fourier de la función. Utilice marcadores verticales para mostrar dónde se producen en relación con la frecuencia de muestreo.
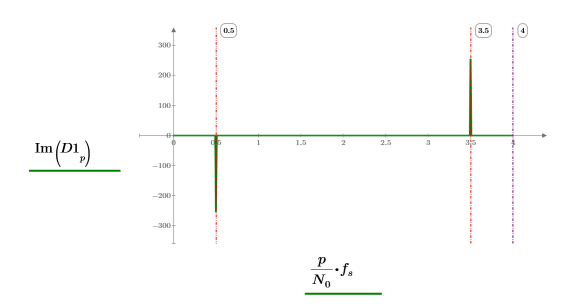
Señal de pulso cuadrado (boxcar)
1. Utilice la función escalón de Heaviside Φ para definir una señal de pulso cuadrado.
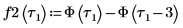
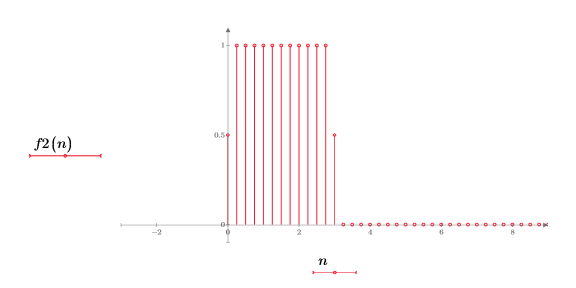
2. Trace los primeros elementos de la función f2.
3. Utilice la función dft para buscar la transformada de Fourier discreta de la señal de pulso cuadrado.
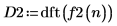
4. Trace la transformada de Fourier de la señal de pulso cuadrado. Utilice marcadores verticales para mostrar dónde se producen en relación con la frecuencia de muestreo.
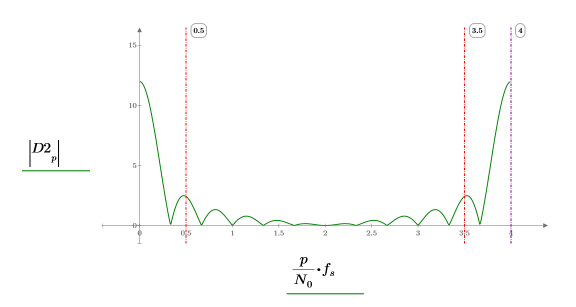
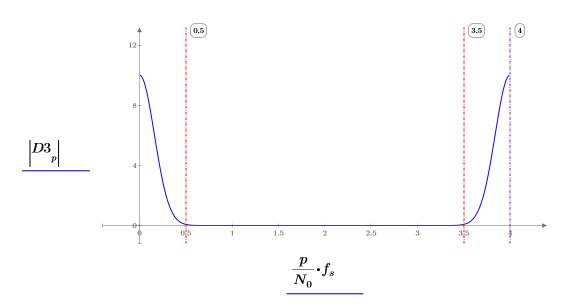
Señal gaussiana
1. Defina la siguiente señal gaussiana.
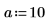
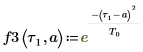
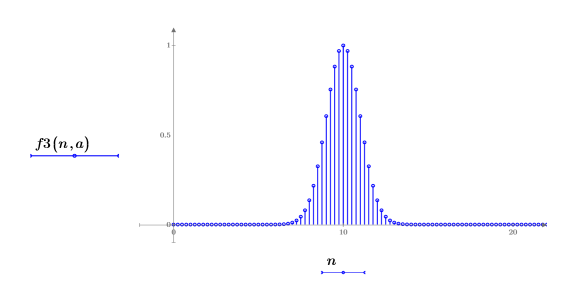
2. Trace los primeros elementos de la función f3.
3. Utilice la función dft para buscar la transformada de Fourier discreta de la señal gaussiana.
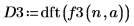
4. Trace la transformada de Fourier de la señal gaussiana. Utilice marcadores verticales para mostrar dónde se producen en relación con la frecuencia de muestreo.