Ejemplo: vectores propios y autovalores
Utilice las funciones eigenvals, eigenvecs y eigenvec para buscar los autovalores y los vectores propios de una matriz real o compleja. Compruebe la teoría de que para una matriz cuadrada M, un vector diferente a cero v es un vector propio de M si se puede encontrar un número λ que:
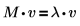
1. Defina una matriz cuadrada de entrada.
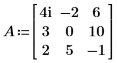
2. Llame a eigenvals y eigenvecs para obtener los autovalores y vectores propios de la matriz A.
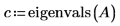
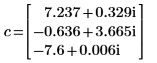
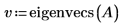

La primera columna de v es el vector propio que corresponde al primer elemento de c. De forma similar, la segunda columna de v es el vector propio que corresponde al segundo elemento de c, y así sucesivamente.
3. Defina v1 en el primer vector propio y c1 en el primer autovalor de A. Compare A x v1 con c1 x v1.
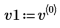
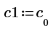
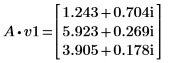 | 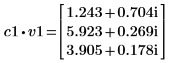 |
4. Defina v2 en el primer vector propio y c2 en el primer autovalor de A. Compare A x v2 con c2 x v2.
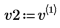
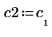
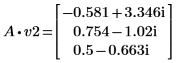 | 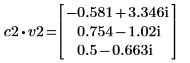 |
5. Defina v3 en el primer vector propio y c3 en el primer autovalor de A. Compare A x v3 con c3 x v3.
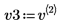
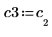
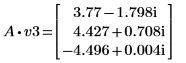 | 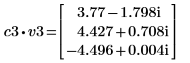 |
6. Llame a la función eigenvec para obtener un solo vector propio para un autovalor determinado.
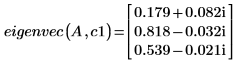

Los resultados que devuelven eigenvecy eigenvecs no coinciden necesariamente, sin embargo, ambas soluciones son válidas. Los vectores propios no son exclusivos. Están relacionados con otros vectores propios mediante un factor de escala. Para un autovalor dado, hay un número infinito de vectores propios.