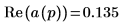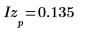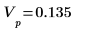Ejemplo: dft e idft de un vector
Use las funciones dft e idft para buscar la transformada de Fourier discreta directa o inversa de un vector.
1. Defina la longitud de un vector de datos.
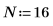
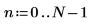
2. Utilice la función exp para crear un vector de datos reales de longitud N.
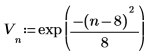
3. Trace los datos.
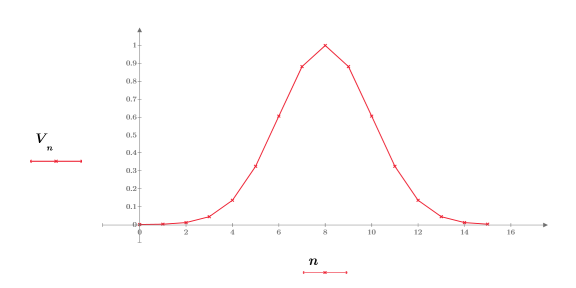
4. Aplique la función dft para calcular la transformada de Fourier discreta de V.
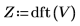
5. Trace los valores absolutos de Z.
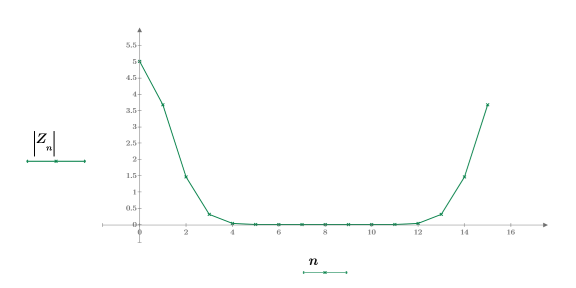
6. Muestre la definición de la función dft.
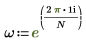
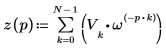
7. Utilice la definición anterior para buscar un elemento de frecuencia específico y compárelo con el elemento correspondiente de la salida de la función dft.
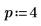
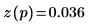
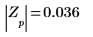
Idft gaussiano
La función idft es la transformada inversa de dft. Acepta un vector real o complejo como argumento y devuelve un vector de la misma longitud.
1. Muestre que la transformada inversa de una función dft es la función en sí.
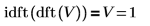
2. Utilice el vector definido anteriormente V y, a continuación, muestre que la inversa de la dft de V es V en sí.
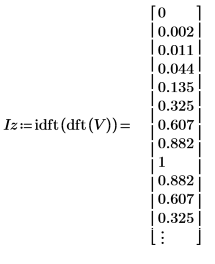 |  |
3. Muestre la definición de la función idft.
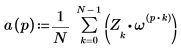
4. Utilice la definición anterior para buscar un elemento de frecuencia específico y compárelo con el elemento correspondiente de la salida de la función idft y el vector V.