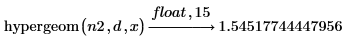Ejemplo: Comparación de las funciones simbólicas Fhyper, Mhyper e Hypergeom
La función hypergeom
1. La siguiente integral se define en términos de la función hypergeom, tal como se indica a continuación:

2. Evalúe el resultado en los extremos del intervalo [1, 2].
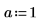 | 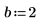 | 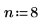 |
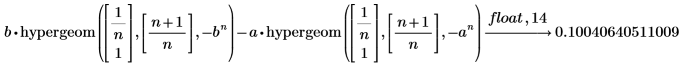
3. Asegúrese de que el resultado numérico anterior concuerde con el valor de la siguiente integral definida equivalente.
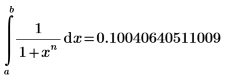
Función mhyper
1. Asigne valores a los parámetros de la función mhyper.
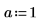 | 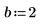 | 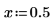 |
2. Evalúe la función en mhyper(a,b,x).
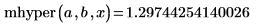
3. Verifique que la función hypergeom devuelva los mismos resultados que mhyper en el caso especial en que:
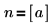 | 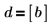 |
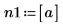 | 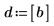 |
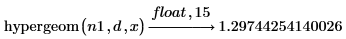
La función fhyper
1. Asigne valores a los parámetros de la función fhyper.
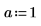 | 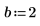 | 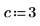 | 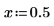 |
2. Evalúe la función en fhyper(a,b,c,x).
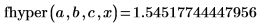
3. Verifique que la función hypergeom devuelva los mismos resultados que fhyper en el caso especial en que:
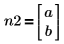 | 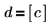 |
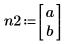 | 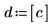 |