Ejemplo: distribución de Cauchy
1. Muestre la definición de la distribución de Cauchy:
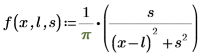
Donde:
◦ l es el parámetro de ubicación (mean)
◦ s es el parámetro de escala (raíz cuadrada de la varianza), s > 0
2. Defina tres conjuntos de parámetros de ubicación y escala y, a continuación, calcule la amplitud, o la altura, de la curva con los parámetros de ubicación y escala l0 y s0:
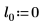 | 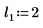 | 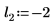 |
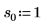 | 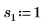 | 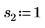 |
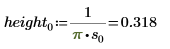
3. Utilice la función dcauchy para obtener la densidad de probabilidad del valor x usando distintos valores de parámetros de ubicación y un parámetro de escala fijo:
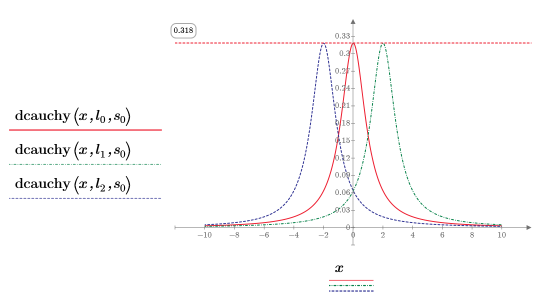
Los distintos valores de los parámetros de ubicación desplazan la curva a lo largo del eje X.
4. Trace la función dcauchy mediante un parámetro de ubicación fijo y distintos valores de parámetros de escala:
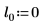 | 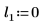 | 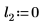 |
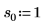 | 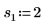 | 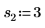 |
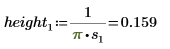
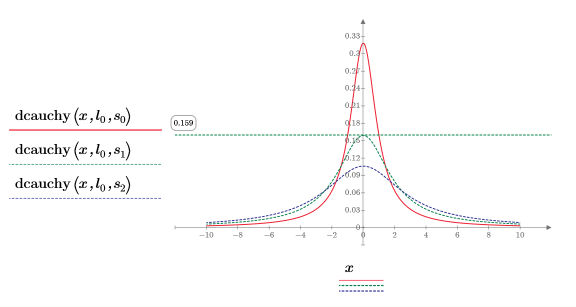
Los distintos valores de parámetros de escala cambian la altura de la curva.
5. Trace la función dcauchy usando los distintos valores de parámetros de ubicación y escala:
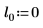 | 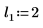 | 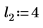 |
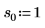 | 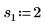 | 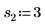 |
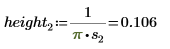
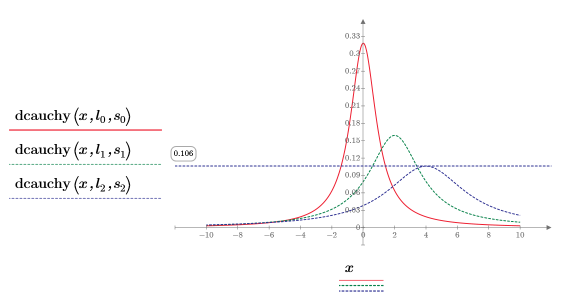
Los distintos valores de los parámetros de escala y ubicación desplazan las curvas y cambian su altura.
6. Trace la función pcauchy usando los distintos valores de parámetros de ubicación y un parámetro de escala fijo:
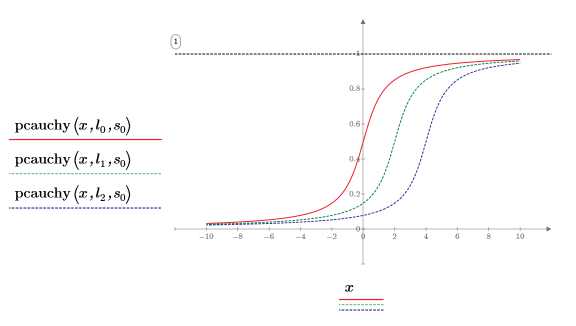
◦ Los distintos valores de los parámetros de ubicación desplazan la curva a lo largo del eje X.
◦ Todos los valores y de pcauchy se encuentran entre 0 y 1.
7. Trace la función pcauchy mediante un parámetro de ubicación fijo y distintos valores de parámetros de escala:
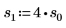
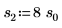
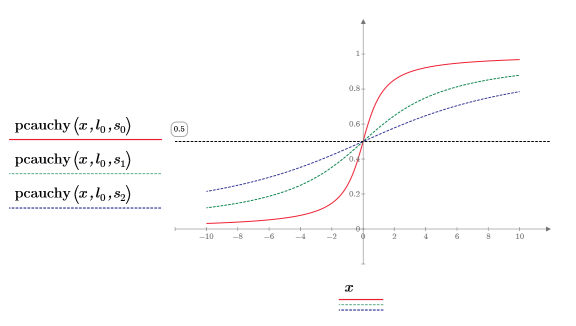
◦ Los distintos valores de los parámetros de escala aplanan la curva horizontalmente, pero todas las curvas se cruzan en y=0.5.
◦ Todos los valores y de pcauchy se encuentran entre 0 y 1.
8. Trace la función qcauchy usando los distintos valores de parámetros de ubicación y un parámetro de escala fijo:
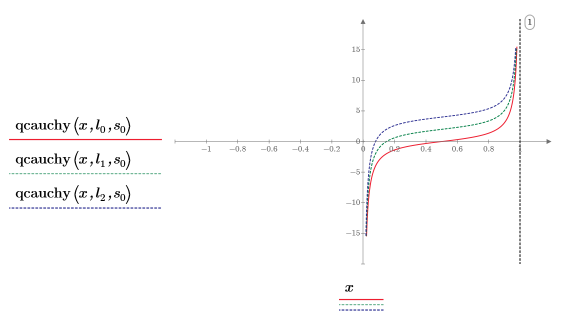
◦ Los distintos valores de los parámetros de ubicación desplazan la curva a lo largo del eje Y.
◦ Todos los valores x de qcauchy se encuentran entre 0 y 1.
9. Calcule la función rcauchy usando parámetros de ubicación y de escala fijos:
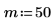
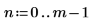
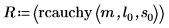
La función rcauchy devuelve un vector de m números aleatorios con distribución de Cauchy.
10. Trace los números aleatorios que ha devuelto la función rcauchy.
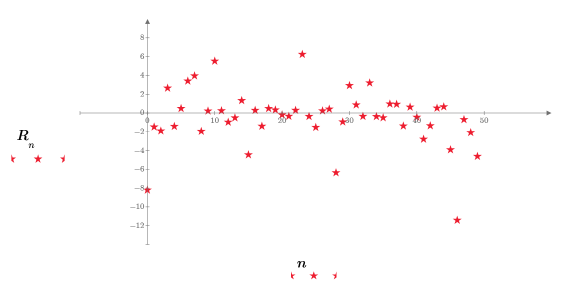
Al volver a calcular la hoja de trabajo, la función rcauchy devuelve un nuevo conjunto de números aleatorios y el gráfico se actualiza en consecuencia.