Ejemplo: Análisis de varianza (ANOVA) para factoriales no replicados
Utilice la función anova para realizar un análisis de varianza para un factorial no replicado mediante la detección de un factor insignificante y la posterior proyección del factorial en un factorial de menor orden.
1. Llame a la función fullfact para crear una matriz de diseño factorial completa para realizar un experimento que pruebe la velocidad de filtración de una planta piloto. Los factores A, B, C y D corresponden a la temperatura, la presión, la concentración de formaldehído y el índice de agitación, respectivamente.
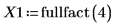
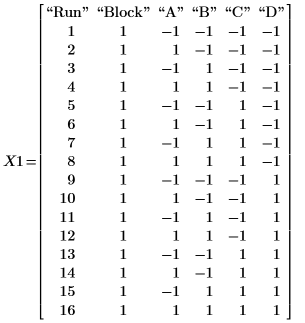
2. Registre los resultados del experimento en la matriz Y1 con un elemento por cada una de las dieciséis ejecuciones.

3. Llame a la función quickscreen para obtener la respuesta media de cada factor principal.

4. Cree un gráfico de efectos para determinar los factores significativos.
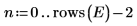
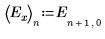
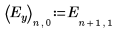
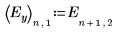

El factor C y las interacciones de segundo orden que incluyen C tienen solo un pequeño impacto sobre el experimento. En comparación con los factores A, B y D, el factor C no es significativo.
5. Llame a la función anova para realizar un análisis de varianza.
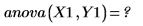
La función anova devuelve un error porque Y1 no está replicado. Sin embargo, dado que C no es significativo, “Run 1” y "Run 5" son duplicados en lo que se refiere a los factores A, B y D. Este es también el caso de “Run 2" y "Run 6". De hecho, la matriz de diseño ABCD 24 en su totalidad contiene un duplicado de la matriz de diseño ABD 23 cuando C no es significativo.
6. Llame a la función fullfact para crear una matriz de diseño factorial 23 completa.

En X2, se cambian los nombres de factor. Los factores iniciales A, B, D pasan a ser A, B, C.
7. Reorganice los resultados del experimento para ajustarlos a un experimento factorial de 23.
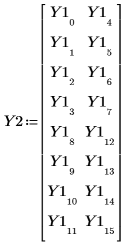
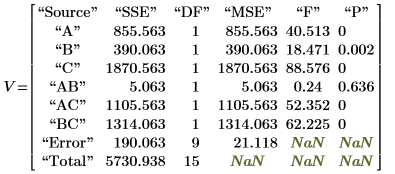
8. Llame a la función anova utilizando Y2.
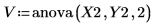
9. Utilice la función qF para calcular el F-value crítico de los factores y las interacciones, y comparar su F-value con el F-value crítico.
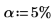
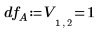
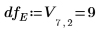
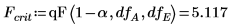
◦ En el gráfico de efectos se indica que el factor C no es significativo en comparación con A, B y D.
◦ Los factores A, B, D (se muestra en V como A, B, C) y sus interacciones AD, BD (se muestra en V como AC, BC) son significativos en el nivel 5 % ya que sus F-values son mayores que Fcrit. Este análisis de varianza refuerza la conclusión subjetiva que se deriva del gráfico de efectos.
Referencia
Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, New York, 2001, págs. 246.