Ejemplo: 1 factor de análisis de varianza (ANOVA)
Utilice la función fullfact para diseñar un experimento y la función anova para analizar el resultado del experimento.
1. Defina el número de factores de un experimento que comprueban el efecto de la cantidad de fibra de algodón sobre la resistencia de una fibra sintética nueva.
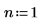
2. Defina la configuración de algodón utilizada en el experimento.
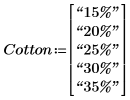
3. Utilice la función length para definir el número de niveles del factor.
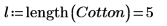
4. Llame a la función fullfact para crear una matriz de diseño factorial completa que represente al experimento y sus ejecuciones.
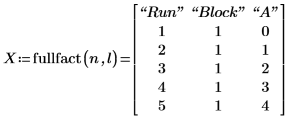
En la matriz de diseño X, A representa el factor de algodón y sus niveles se muestran en un formato codificado:
Valores codificados de A | Valores reales de A |
|---|---|
0 | 15% |
1 | 20% |
2 | 25% |
3 | 30% |
4 | 35% |
5. Mida la resistencia de la fibra sintética en la primera ejecución, cuando el espesor de la fibra de algodón es del 15 %.
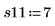
6. Tome medidas en las otras cuatro ejecuciones.
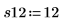
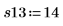
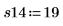
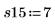
7. Llame a la función randomize para cambiar el orden de ejecución.
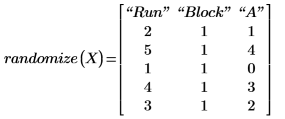
8. Replique las medidas en el orden que especifique la función randomize.
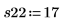
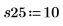
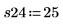
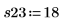
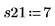
Es útil repetir los experimentados para obtener una media del efecto de las variables no controladas. Llame a la función randomize antes de repetir los experimentos para reducir cualquier tipo de correlación entre los factores de entrada.
9. Repita los pasos 7 y 8 para todas las réplicas que desee. Registre todas las medidas en la matriz Y.

Cada columna contiene los datos de una de las réplicas y cada fila, los datos de una ejecución determinada.
10. Llame a la función boxplot para preparar los datos para un gráfico de caja que tenga una caja para cada ejecución.
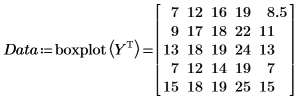
La matriz Y se transpone porque los resultados de cada ejecución se registran en filas de la matriz, pero los conjuntos de datos que se proporcionan a boxplot deben ser columnas de matriz.
11. Llame a la función boxplotgraph.
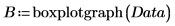
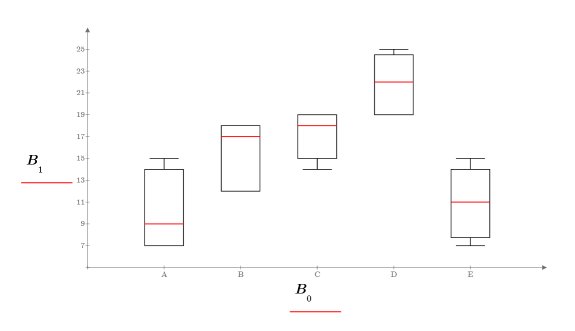
12. Cree un gráfico de caja.
a. Trace la salida de la función boxplotgraph:
b. Cree regiones de texto con los rótulos de cada factor:
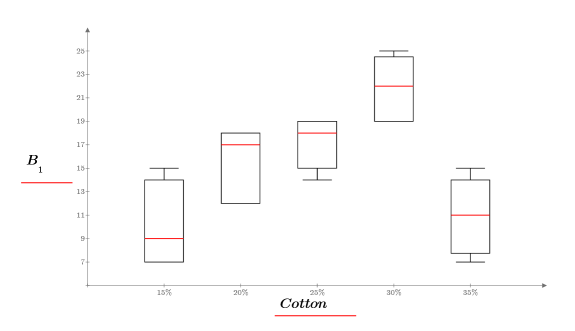
Al observar el gráfico de caja, parece que el porcentaje de espesor del algodón afecta a la resistencia a la tracción de la fibra. La resistencia a la tracción de la fibra alcanza un punto máximo cuando el espesor del algodón es aproximadamente un 30 % del espesor de la fibra.
13. Llame a la función anova para comprobar si el porcentaje de espesor del algodón afecta a la resistencia a la tracción.

14. Defina r como el número de ejecuciones y x como el número de réplicas y, a continuación, calcule la suma de cuadrados de la columna SSE.
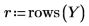
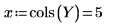
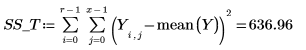
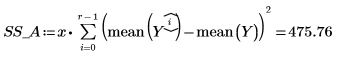
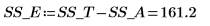
15. Defina N como el número total de medidas y, a continuación, calcule los grados de libertad de la columna df.
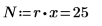
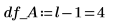
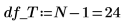
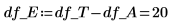
16. Calcule los cuadrados medios de la columna MSE.
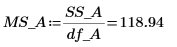
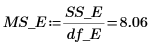
17. Calcule el F-value del factor A.
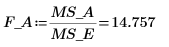
El P-value de la columna P es menor que 0.05, lo que indica que el factor A es significativo.
18. Utilice el F-value para probar la hipótesis de que A es un valor significativo. Calcule el valor F crítico para un nivel de significancia del 5%.
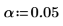
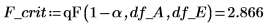
El F del factor F-value es mayor que el valor A crítico, lo que confirma una vez más que el porcentaje de espesor del algodón influye en la resistencia a la tracción de la fibra.
Referencia
Montgomery, D.C., Design and Analysis of Experiments, 5th ed., John Wiley & Sons, Nueva York, 2001. 62.