To Write the Continued Fraction Expansion for a Number or Function
• Place the cursor at the end of a number or function, insert the symbolic evaluation operator, and type the keyword confrac. PTC Mathcad returns the answer as a column vector.
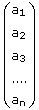
The column vector represents the following continued fraction:
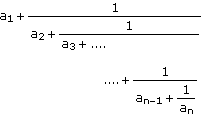
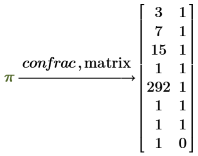
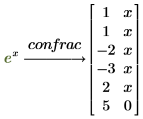
PTC Mathcad returns a column vector when you apply the confrac keyword to an expression containing only numbers, but it returns a two-column matrix if the expression contains a variable.
• To return the answer as a fraction rather than as a vector, use the modifier fraction.
By default, PTC Mathcad returns enough terms of the continued fraction so that the result is accurate to within 10 significant digits. You can specify a different accuracy for the result by typing a comma after confrac followed by a positive integer for the number of significant digits.
Get the continued fraction expansion of the constant π:
Column Vector | Continued Fraction |
|---|---|
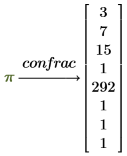 | 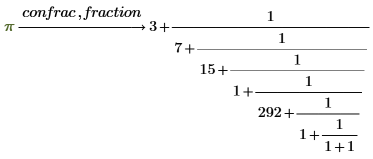 |
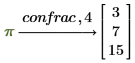 | 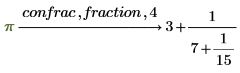 |
• To return the answer as a matrix with two columns in which the second column contains the partial numerators of the continued fraction, use the modifier matrix.
• Get the continued fraction expansion for the Taylor series:
Column Vector | Continued Fraction |
|---|---|
 | 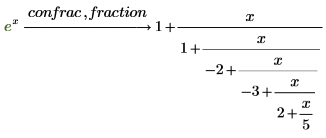 |
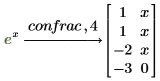 |  |