Example: Symbolic Calculus II
Solve symbolic problems in calculus by evaluating the expression for the problem using the symbolic evaluation operator and adding keywords to modify the problem, if necessary.
Taylor and Maclaurin Series
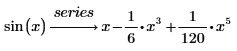
By default, PTC Mathcad returns the terms up to order 6, so that the highest power in the answer is 5. |
2. Type a comma after series and then type x, 10 in the placeholder to increase the order of the terms to 10.
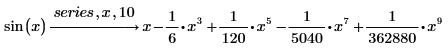
3. Expand the sin function into a Taylor series about 1.
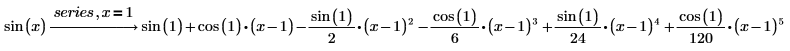
4. Expand a function in more than one variable around the point (x, y)=(0, 1).
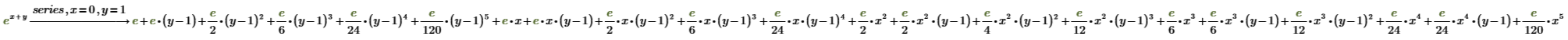
5. Display the coefficients as four-digit numbers instead of in terms of e.
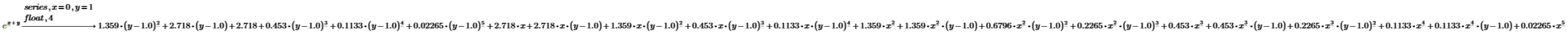
Partial Fractions
1. Perform a partial fraction decomposition of a rational function (quotient of polynomials) using the keyword parfrac.
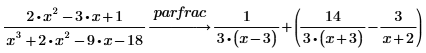
2. Perform a partial fraction decomposition of a function that is defined via the range product operator.
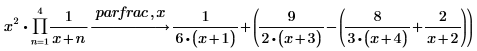
Decomposition over the Real or Complex Numbers
By default, PTC Mathcad performs the partial fractions decomposition over the field of rational numbers. That is, if the initial expression is a quotient of polynomials with rational coefficients, the polynomials in the result also have rational coefficients.
1. Use the keyword parfrac to find the fractions of the following function.
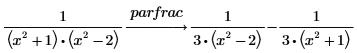
2. Perform further decomposition of one of the terms in the following expressions:
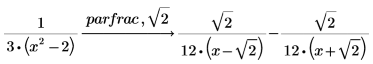
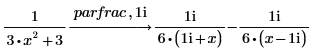
3. Perform a complete partial fractions decomposition of a rational function over the complex numbers by typing domain = complex after parfrac.
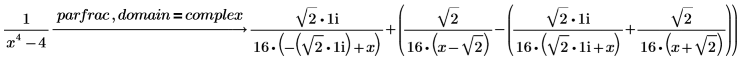
Perform these steps to get a decomposition over the real numbers: a. Combine the last two terms into a single term with real coefficients, using the keyword simplify as follows: 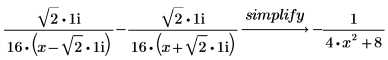 b. Replace the simplified results into the original results to get the following result: 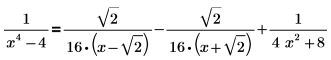 |
Continued Fractions
1. Use the keyword confrac to find the continued fraction expansion of a number.
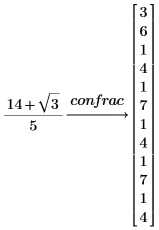
2. Use the modifier fraction to see the actual continued fraction rather than the vector.
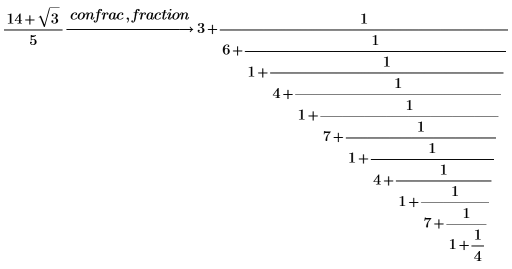
By default, PTC Mathcad returns enough terms of the continued fraction so that the answer is accurate to 10 significant digits. |
3. Add a positive integer specifying the number of significant digits to return results with a different degree of accuracy.
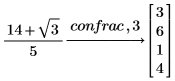

4. Expand the sin function as a continued fraction.
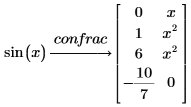
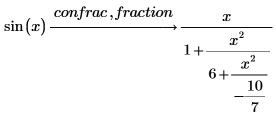
PTC Mathcad returns a second column containing the powers of x corresponding to the terms. |