ODE Function
• odesolve(vf, b, [intvls])—Defines a function that represents the solution to a system of Ordinary Differential Equations (ODE), subject to initial value or boundary value constraints. The ODEs must be linear in their highest derivative term, and the number of initial and boundary conditions must equal the order of the ODEs.
Arguments
• vf is a function or a column vector of functions as they appear within the solve block.
You must include the list of arguments when you define the functions in vf. For example, if you are solving for the functions f(t) and g(t), you enter vf as follows:
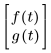
• b is the real terminal point of the integration interval. b can be greater than or less than the initial value which is defined in the solve block.
• intvls (optional) is the integer number of discretization intervals used to interpolate the solution function. The number of solution points is the number of intervals + 1. The default value of intvls is 1000.
The default value of intvls is usually large enough to give an accurate interpolated solution, but you can increase this value to capture fine details in the solution. Doing so requires odesolve to save more points for interpolation, and might increase calculation time.
If you are solving the ODE over a large interval, set intvls to a value larger than the default.
Units and Dimensions
You can use units in odesolve functions and constraints. The following rules apply for units and dimensions:
• Dimensions must be consistent through the solving process. If t is of argumentDimension and f(t) is of valueDimension,
then
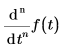 must be of valueDimensions/argumentDinemsionsn.
must be of valueDimensions/argumentDinemsionsn.For example: t is in seconds and f(t) is in meters, then
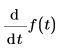 is in m/s and
is in m/s and is in m/s2.
is in m/s2.• The initial value and terminal point of the integration interval must be of the same dimension as the function argument.
• The number of discretization intervals is always unitless.
Additional Information
• Function odesolve can only be used inside a solve block.
• Legacy PTC Mathcad function Odesolve is interchangeable with its lowercase counterpart.
• Inserting the lowercase function from the Ribbon, or manually typing the lower/upper case version, automatically assigns it the Keyword label.
• The odesolve function uses the Adams/BDF solving algorithm.
• When inside a solve block, odesolve is not affected by the value of TOL.