Example: Zero-Phase Filtering
Use the filtfilt function to compute the zero-phase response of a filter, using a "forward-backward" filtering model.
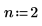
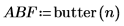
2. Use the iirlow function to get the coefficients for a lowpass IIR filter with cutoff frequency of 0.25.
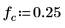
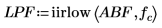
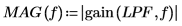
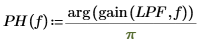
4. Redefine the magnitude and phase response of the filter for all values of f, but in terms of p.
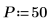 | 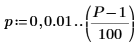 |
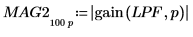 | 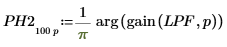 |
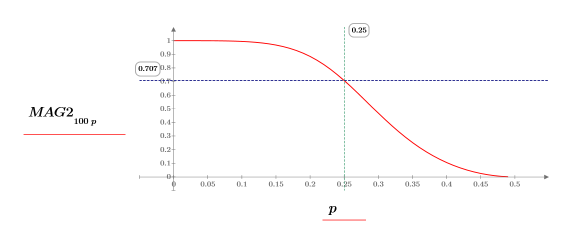
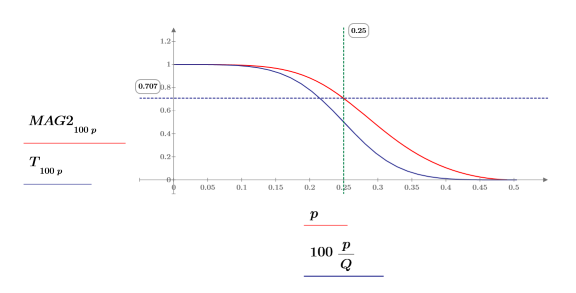
5. Plot the magnitude response, and then use markers to show its magnitude at the cutoff frequency.
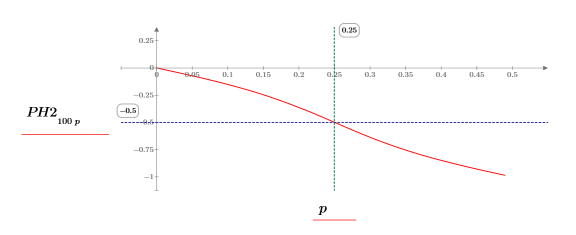
6. Plot the phase response, and then use markers to show its value at the cutoff frequency.
7. Define and plot a sample pulse signal.
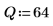 | 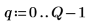 | |
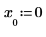 | 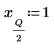 | 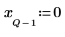 |
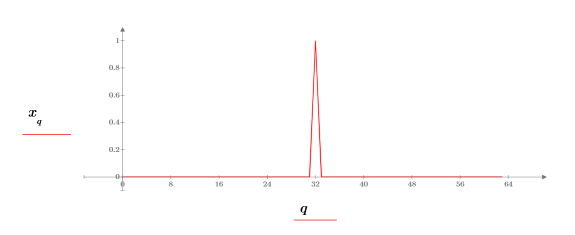
The input is comprised of an impulse at the midpoint of the signal.
8. Use the filtfilt function to calculate the zero-phase output.
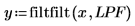
9. Use the dft function to see the effect that the filter has on the signal by computing the Fourier transforms of both signals and plotting the magnitude and phase of Y.
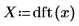
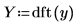
10. Use the mag function to show that the transfer function, given by the ratio of magnitudes of X and Y, has the expected Butterworth cutoff shape.
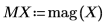
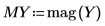
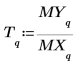
11. Plot the magnitude response along with the transfer function.
12. Use the arg function to define the phase difference between the principal arguments of X and Y.
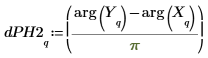
13. Plot the magnitude response and the phase difference between X and Y.
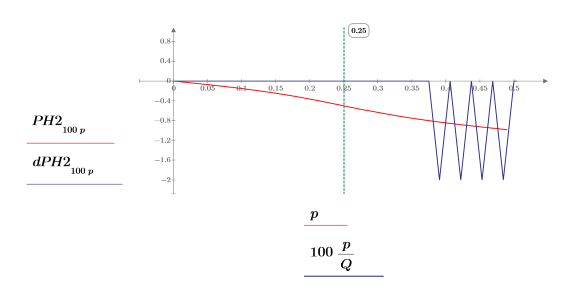
• The effect of the filtfilt function is to double filter the signal magnitude, as shown in the plot, but the phase shift is zero instead of the nonlinear phase of the original filter.
• When interpreting the phase plot, remember that phases of -2π and 0 are equivalent. When the magnitude of Y is very small, as it is for frequencies far above the cutoff, the phase can be meaningless due to numerical noise.