Example: Residual Analysis
Calculate the residuals of a data set to check if the set is linearly distributed. Before using the regression model for prediction, check that the linear model assumptions have been met:
• The errors must be uncorrelated.
• For any given value of X, the errors should be normally distributed with a mean of zero and a constant variance.
Standardized Residuals
To interpret the relative magnitude of the residuals, you can standardized them. You need to divide the residuals by an estimate of the error standard deviation.
1. Define the following data set:
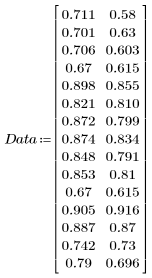
2. Plot the data set.
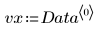
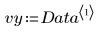
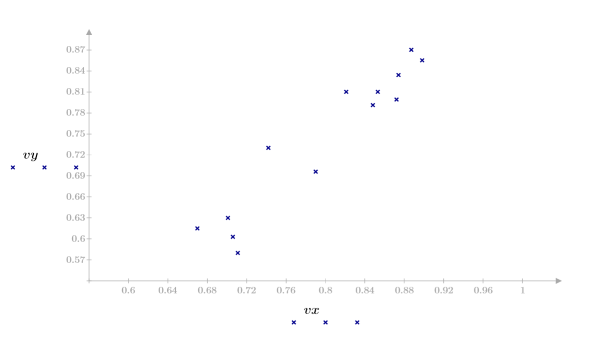
The data seems linear. This is confirmed by the correlation coefficient being close to 1:
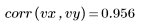
3. Define the line of best fit:
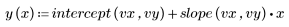
4. Subtract the fit values from the measured values.
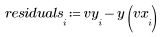
5. Divide the residuals by the standard error of the estimate.
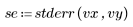
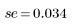
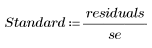
Studentized Residuals
Studentized residuals, or adjusted standardized residuals, are another frequently used estimate for the standard error. This estimate adjusts for the distance between each value of x and the mean of x.
1. Calculate the distance between the values and the mean.
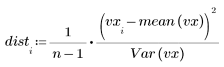
2. Define the standard deviation leveraged for each residual.

3. Define the studentized residuals:
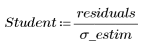
Studentized residuals are more precise than standardized residuals, because they account for any point-to-point differences in error variance. Nevertheless, the residuals are usually close in value:
 |  |
4. Call polyfitstat. Display the submatrix of observation diagnostics which contains the studentized residuals.
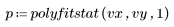
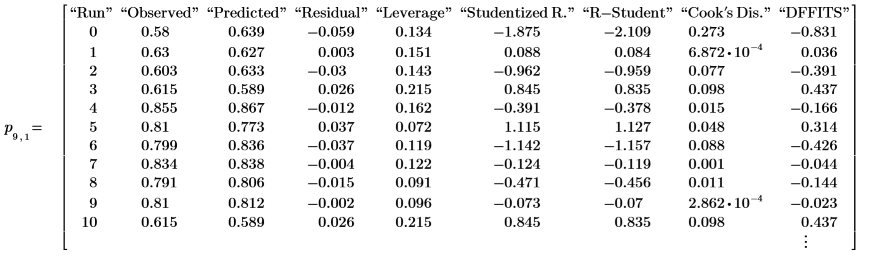
Checking for Linearity
Check that the Data set is linearly related. Create a counter example using a random sample having a curvilinear relationship. If the data are linearly related, and the errors are normally distributed, the scatter plots have no discernible pattern. The points are randomly scattered about the hypothesized error mean of zero.
1. Plot the residuals against the x values and against the predicted y values.
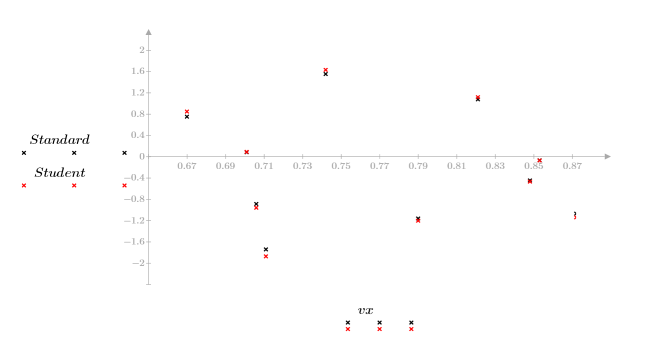
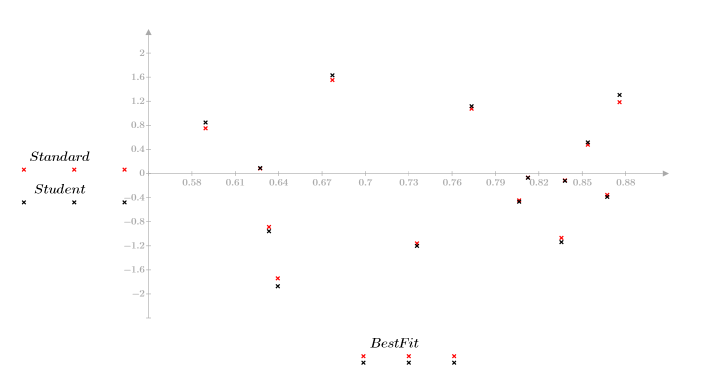
The lack of pattern of the residuals indicates that the data is linearly related.
2. Generate a random sample of points that have a quadratic relationship.
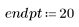
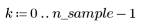
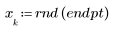
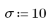
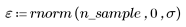
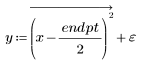
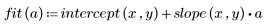
3. Plot the relative magnitude of the residuals.
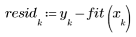
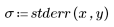
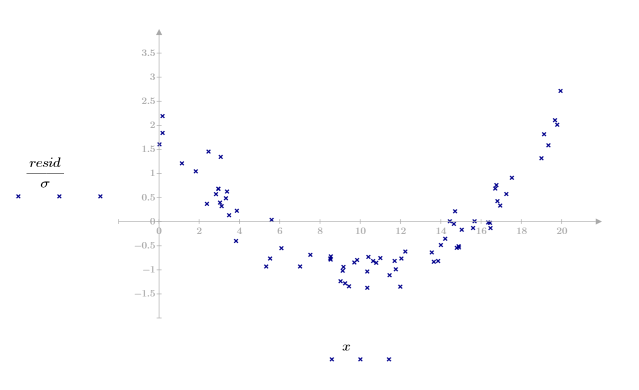
The quadratic pattern in the data is reflected in the residual scatter plot. This data is not linearly related.
Checking for Constant Error Variances
No pattern in the error variances was detected in the Data set. Create a counter example where the data appears linear but the error variances are not normally distributed, and a scatter plot of the residuals shows either an increasing or decreasing spread from left to right.
1. Generate a random sample of points that are increasingly scattered from left to right.
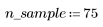
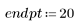
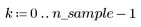
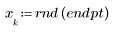
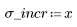
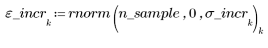
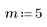
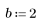
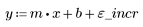
2. Calculate a line of best fit. Plot the random data set and the fit function.
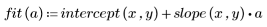
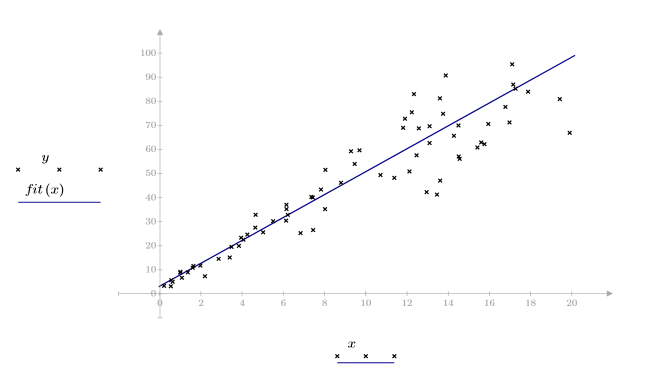
The correlation coefficient close to 1 indicating that the data is linearly related:
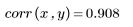
3. Plot the relative magnitude of the residuals.
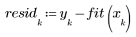
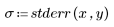
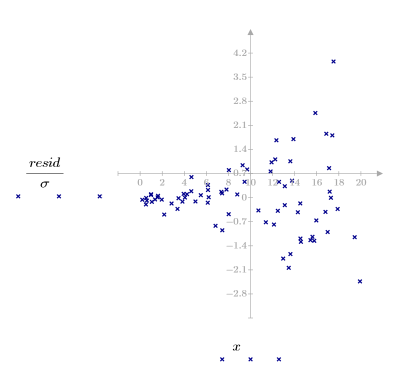
The scatter plot of residuals does not appear randomly distributed. The points in the residual plot are increasingly scattered from left to right.
Checking for Correlation of Errors
You can check if adjacent error terms in the linear regression model are correlated by using the Durbin-Watson statistic.
Calculate the Durbin-Watson statistic for the Data set:
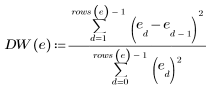
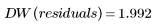
Values for the Durbin-Watson statistic range from 0 to 4. If adjacent terms are uncorrelated, the Durbin-Watson value is close to 2. Durbin-Watson values less than 2 indicate positive adjacent correlations, and values greater than 2 indicate negative correlations.
The Durbin-Watson statistic is used in the calculation of least-squares B-splines. Unfortunately, the Durbin-Watson statistic cannot detect higher-order (non-adjacent) correlations. These types of correlations do not commonly occur without a correlation between adjacent errors.
The Durbin-Watson statistic is one of the statistics returned by polyfitstat:
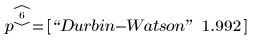
Checking for Normality
Check if the Data set is normally distributed by creating a normal plot of the standardized residuals.
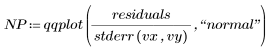
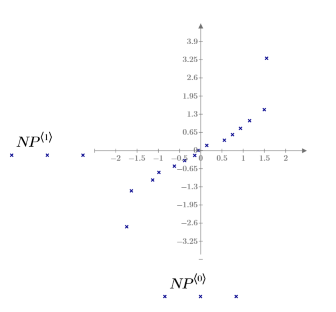
The normal plot resembles a straight line. The errors are therefore approximately normally distributed. Since normal plots can be sensitive to other assumption violations, such as when the error variances are not equal, it is best to check for normality last.