Statistics of Multivariate Polynomial Regression
• polyfitstat(X, Y, n/"terms"/M, [conf])—Returns statistical data on a polynomial regression model fitting the results recorded in matrix Y to the data found in matrix X. You can define the polynomial regression equation by its polynomial order n or by its terms as specified in the string “terms” or in matrix M. Use matrix M when you do not want to include the intercept in the polynomial fit. Use the optional argument conf to specify a confidence interval other than the default 95%.
The second column of the matrix returned by polyfitstat contains the following elements:
|
Row
|
Description
|
|---|---|
|
1
|
The standard deviation for Y
|
|
2, 3, 4
|
R2, adjusted R2, and predicted R2
|
|
5
|
PRESS—Prediction error sum of squares (useful for scaling residuals)
|
|
6
|
Durbin-Watson test statistic for autocorrelation
|
|
7
|
Matrix of regression coefficients as returned by polyfitc
|
|
8
|
Matrix of ANOVA for the regression model with columns identical to the table of results returned by anova, and with the following rows:
• Regression—Subtotal, which is then broken down for each term (excluding the intercept)
• Residual (Error)—Subtotal, which is then broken down between the Lack of Fit error and the Pure Experimental error
• Total for the regression model
|
|
9
|
Matrix of diagnostics with the following columns:
1. Numbering for each run or data point
2. Observed result for each run or data point
3. Predicted result by the regression model under investigation
4. Residual—Difference between the observed and the predicted result
5. Leverage—Measure of the distance between the observed result and the point that is at the center of all the observed results
6. Studentized residual—Residual divided by the variance based on the observed result
7. R-student—Residual divided by the variance based on a data set where the observed result is removed
8. Cook’s distance—Measure of the influence of the observed result on all the other data points
9. DFFITS—Difference between the result predicted by a regression model based on a data set where the observed result is included and between the result predicted by another model where the observed result is removed
|
Arguments
• X is a design matrix or a matrix in which each column represents an independent variable. Each column of X must have compatible units.
• Y is a vector or a matrix of measured or simulated results with each row containing the results for each run or data point defined in X. When the rows do not all contain the same number of replicates, you must pad the empty elements of Y with NaNs. The elements of Y must have compatible units.
• n is an integer specifying the polynomial order. It must be smaller than the total number of data points: 1 ≤ n ≤ length(Y) − 1. Otherwise, the problem is under constrained with no unique solution.
• “terms” is a string specifying the terms, or the factors and interactions, to include in the polynomial regression. “A B AB AA BB” means that the polynomial contains the following terms:
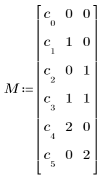
c0 + c1∙A + c2∙B + c3∙A∙B + c4∙A2 + c5∙B2
For the separators, you can use a space, a comma, a colon, or a semicolon.
• M is a matrix specifying a polynomial with guess values for the coefficients in the first column and the power of the independent variables for each term in the remaining columns. For the polynomial described above, define M as follows:
• conf (optional) is the desired confidence limit, a percentage expressed as a number between 0 and 1, inclusive. By default, conf = 0.95 for a 95% confidence interval.