Example: Parametrizing Solutions
Define a function that solves an equation or a system dependent on an unknown parameter with either the root function or a solve block. This allows you to solve a whole family of equations.
Root Function
Solve the equation f1=f2 for different values of parameter a.
1. Define two functions.
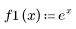
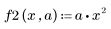
2. Define a new function, S, to solve the equation for different values of a.
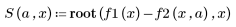
3. Define an initial guess value.
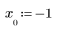
4. Define the range of parameter a and solve the equation for each of its values.
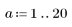
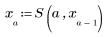
 |  | 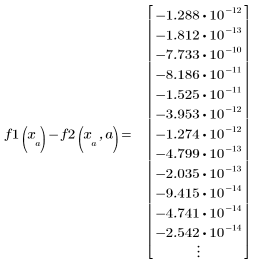 |
Solve Block: Friction Factor
Find the friction factor f for given values of e (pipe roughness), D (pipe diameter), and R (Reynolds number).
1. Define a guess value.
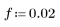
2. Write a solve block to define a function that calculates the friction factor.

Parameters e, D, and R have not yet been defined. Every time you calculate the function FricFac, you can specify new values for these parameters, and the solve block is called again.
3. Calculate the friction factor for various Reynolds numbers.
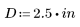
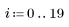
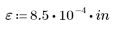
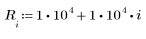
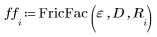
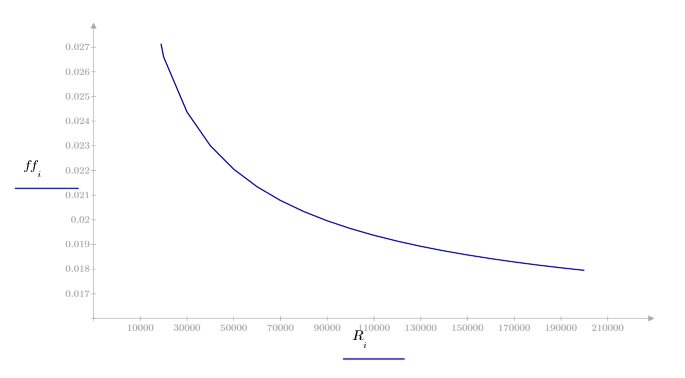
Solve Block: Intersection of Circle and Line
1. Find the points where a circle and line y = 2 - x meet as the radius of the circle varies.
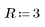
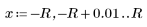
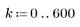
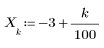
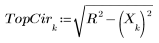
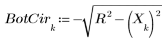
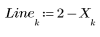
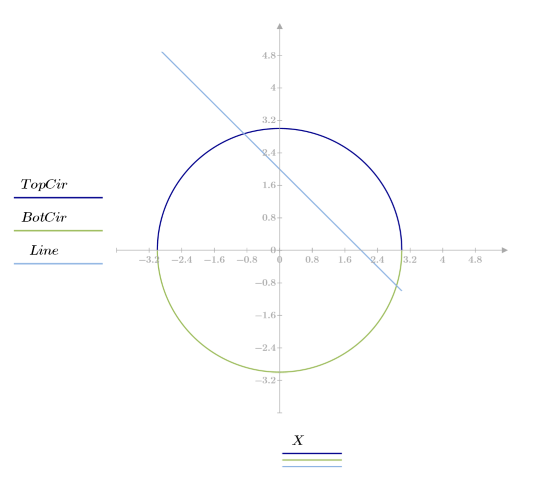
2. Write a solve block to define a function that returns the coordinates of the point of intersection between the line y = 2 - x and the circle of radius R.
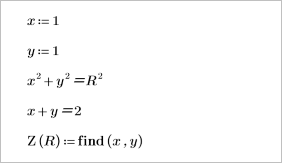
3. Use the newly-defined Z function to find the coordinates of the point of intersection for R=3 and guess values of x=1 and y=1.
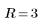
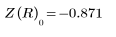
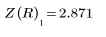
4. Plot the intersection point.
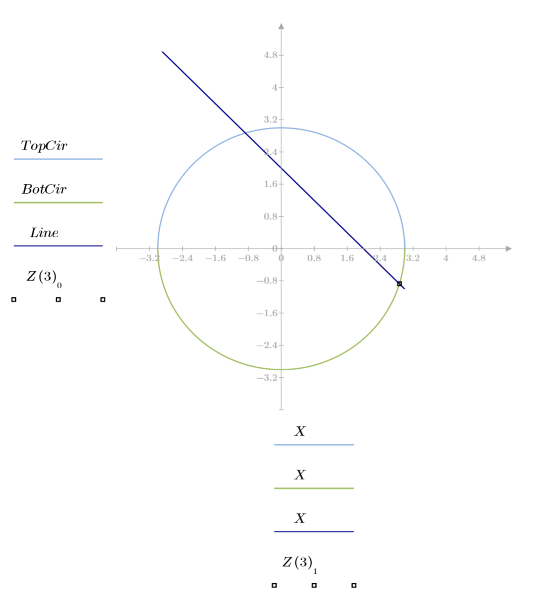
5. Use the newly-defined Z function to find the coordinates of the points of intersection for 5 different values of radius R.
 | 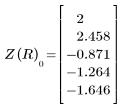 |  |
You can parameterize the above solve block on the guess values as well, by defining Z(R, x, y). This allows you to solve for the two different solutions for each radius using a single solve block setup.